Question 1160681: An opaque bag contains 5 green marbles, 3 blue marbles, and 2 red marbles. Two marbles are randomly drawn without replacement.
A. 1/5
B. 3/10
C. 2/9
D. 1/3
The question and the answer choices in the link here: https://i.imgur.com/CdhrAdS.png
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
there are  green marbles, green marbles, 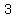 blue marbles, and blue marbles, and  red marbles-> total red marbles-> total 
as I can see on a link, you need to draw twice
in first draw you need  red: red:
if total number of marbles is and you have and you have  red marbles: red marbles:
probability to draw one is 
second draw you want  blue: blue:
we have  blue marbles and total number of blue marbles and total number of  marbles (remember one red is gone,there is no replacement) : marbles (remember one red is gone,there is no replacement) :

probability to draw one red and one blue: 
since there is no such a choice in given options, I will try to see what is the probability of choosing two green marbles
there are  green marbles, green marbles, 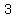 blue marbles, and blue marbles, and  red marbles-> total red marbles-> total 
to draw, for example, one green marble, probability is 
since without replacement, now total number of marbles is  and total number of green marbles is and total number of green marbles is 
and, to draw one more green marble without replacement , probability is 
then, the probability of two green marbles is:

for an answer you have option:
C.  (in case you want to draw two green marbles) (in case you want to draw two green marbles)
|
|
|