Question 1160259: How many four-character passwords can be formed using the characters A, B, C, 1, 2 if the characters can be repeated? Thank you.
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are 5 characters, so if they can all be repeated, the number of first letters is 5*number of second letters (still 5)*etc.
It is 5^4=625
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You have 5 opportunities to place any of 5 symbols A, B, C, 1, 2 in the first (leftmost) position.
You have 5 independent opportunities to place any of 5 symbols A, B, C, 1, 2 in the next, second position.
Thus placing 5 symbols independently in two positions, you have 5*5 = 25 opportunities.
Then you have 5 independent opportunities to place any of 5 symbols A, B, C, 1, 2 in the next, third position.
Thus placing 5 symbols independently in three positions, you have 5*5*5 = 125 opportunities.
Then you have 5 independent opportunities to place any of 5 symbols A, B, C, 1, 2 in the next, fourth position.
Thus placing 5 symbols independently in four positions, you have 5*5*5* = 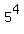 = 625 opportunities.
It means that in all, you may have = 625 opportunities.
It means that in all, you may have 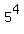 different four-character passwords under the given conditions. ANSWER different four-character passwords under the given conditions. ANSWER
------------
It is a standard mantra solving such problems.
MEMORIZE it (!)
|
|
|