SOLUTION: 1. Find the 25th term of the arithmetic sequence ‒7, ‒4, ‒1, 2, ... 2. In an arithmetic sequence, if a4 = 18 and a10 = 30, determine a1, d, and an. Then write

Algebra ->  Sequences-and-series -> SOLUTION: 1. Find the 25th term of the arithmetic sequence ‒7, ‒4, ‒1, 2, ... 2. In an arithmetic sequence, if a4 = 18 and a10 = 30, determine a1, d, and an. Then write       Log On


   

Question 1160078: 1. Find the 25th term of the arithmetic sequence
‒7, ‒4, ‒1, 2, ...

2. In an arithmetic sequence, if a4 = 18 and a10 = 30, determine a1, d, and an.
Then write the first four terms of the sequence.

3. In a geometric sequence, if a3 = ‒5 and a6 = 40, determine a1, r, and an.
Then write the first three terms of the sequence.
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

1. Find the 25th term of the arithmetic sequence
-7, -4, -1, 2, ...
first term: a%5B1%5D=+-7
second term: a%5B2%5D=-7%2B3=-4
third term:a%5B3%5D=-4%2B3=-1
fourth term: a%5B4%5D=-1%2B3=2
so, common difference is d=3
nth term formula is:
a%5Bn%5D=a%5B1%5D%2Bd%28n-1%29
a%5Bn%5D=-7%2B3%28n-1%29

25th term->n=25
a%5B25%5D=-7%2B3%2825-1%29
a%5B25%5D=-7%2B3%2824%29
a%5B25%5D=-7%2B72
a%5B25%5D=65

2. In an arithmetic sequence, if a%5B4%5D+=+18 and a%5B10%5D+=+30, determine a%5B1%5D, d, and a%5Bn%5D.
Then write the first four terms of the sequence.
a%5Bn%5D=a%5B1%5D%2Bd%28n-1%29....use a%5B4%5D+=+18
18=a%5B1%5D%2Bd%284-1%29
18=a%5B1%5D%2B3d...........solve for a%5B1%5D
18-3d=a%5B1%5D..........eq.1
a%5Bn%5D=a%5B1%5D%2Bd%28n-1%29....use a%5B10%5D+=+30
30=a%5B1%5D%2Bd%2810-1%29
30=a%5B1%5D%2B9d
30-9d=a%5B1%5D..............eq.2
from eq.1 and eq.2 we have
18-3d=30-9d......solve for d
9d-3d=30-18
6d=12
d=12%2F6
d=2
go to eq.1
18-3d=a%5B1%5D..........eq.1, substitute d
18-3%282%29=a%5B1%5D
18-6=a%5B1%5D
12=a%5B1%5D
your nth term formula is:
a%5Bn%5D=12%2B2%28n-1%29
since first term is a%5B1%5D=12 and the difference is d=2, the second is
a%5B2%5D=12%2B2%282-1%29
a%5B2%5D=12%2B2
a%5B2%5D=14
and third term is
a%5B3%5D=14%2B2
a%5B3%5D=16
the first four terms of the sequence are: 12,14,16, 18


3. In a geometric sequence, if a%5B3%5D+=+-5 and a%5B6%5D+=+40, determine a%5B1%5D, r, and a%5Bn%5D.
Then write the first three terms of the sequence.
a%5Bn%5D=a%5B1%5D%2Ar%5E%28n-1%29
use a%5B3%5D+=+-5
-5=a%5B1%5D%2Ar%5E%283-1%29
-5=a%5B1%5D%2Ar%5E2..........solve for a%5B1%5D
a%5B1%5D=-5%2Fr%5E2................eq.1
use a%5B6%5D+=+40
40=a%5B1%5D%2Ar%5E%286-1%29
40=a%5B1%5D%2Ar%5E5..........solve for a%5B1%5D
a%5B1%5D=40%2Fr%5E5................eq.2
from eq.1 and eq.2 we have
-5%2Fr%5E2=40%2Fr%5E5.......solve for r
-5%2F40=r%5E2%2Fr%5E5
-5%2F40=1%2Fr%5E3.......cross multiply
-5r%5E3=1%2A40
r%5E3=40%2F-5
r%5E3=-8
r%5E3=-2%5E3
r=-2
go to
a%5B1%5D=-5%2Fr%5E2................eq.1, plug in r
a%5B1%5D=-5%2F%28-2%29%5E2
a%5B1%5D=-5%2F4
so, nth term formula is
a%5Bn%5D=%28-5%2F4%29%2A%28-2%29%5E%28n-1%29
to write the first three terms of the sequence, we need to find second term
n=2
a%5B2%5D=%28-5%2F4%29%2A%28-2%29%5E%282-1%29
a%5B2%5D=%28-5%2F4%29%2A%28-2%29%5E1
a%5B2%5D=%285%2F4%29%2A2
a%5B2%5D=%285%2Fcross%284%292%29%2Across%282%29
a%5B2%5D=5%2F2
so, the first three terms of the sequence are: 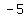-5%2F4,5%2F2, +-5


Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


These are straightforward problems involving arithmetic and geometric sequences; you can do the arithmetic....

1. Find the 25th term of the arithmetic sequence ‒7, ‒4, ‒1, 2, ...

The common difference is +3
The 25th term is the first term, plus the common difference 24 times

2. In an arithmetic sequence, if a4 = 18 and a10 = 30, determine a1, d, and an.
Then write the first four terms of the sequence.

The difference between the 4th term and the 10th term is 30-18 = 12; that difference is 6 times the common difference.
So you can easily find the common difference, d.
Then the first term a1 is the 4th term, minus 3 times the common difference.
Then the formula for an is the first term, plus (n-1) times the common difference.

3. In a geometric sequence, if a3 = ‒5 and a6 = 40, determine a1, r, and an.
Then write the first three terms of the sequence.

The 6th term, 40, is the 3rd term, (-5), multiplied by the common ratio 3 times:
40+=+%28-5%29%28r%5E3%29
r%5E3+=+-8
r+=+-2

You have r; the first term a1 is the third term, -5, DIVIDED BY the common ratio two times; the formula for an is the first term, multiplied by the common ratio (n-1) times.