Question 1157937: The sum of the first three terms in a GP is 38. Their product is 1728. Find the values of the three terms.
My answer were 8 and 18. I want to confirm if it's correct and how will I find the values of the three terms with two solution of a and r
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let "a" be the first term and "r" be the common ratio.
Then from the condition, we have these two equations
a + ar + ar^2 = 38, (1)
a*(ar*)*(ar^2) = 1728. (2)
From equation (2), a^3*r^3 = 1728, or (ar)^3 = 1728, which implies
ar =  = 12; (3)
hence,
r = = 12; (3)
hence,
r = 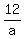 . (4)
Now, in equation (1) replace the term ar by 12, based on (3). You will get
a + 12 + ar^2 = 38, which implies
a + ar^2 = 26. (5)
Next, substitute r = . (4)
Now, in equation (1) replace the term ar by 12, based on (3). You will get
a + 12 + ar^2 = 38, which implies
a + ar^2 = 26. (5)
Next, substitute r = 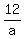 into equation (5), replacing "r" there. You will get into equation (5), replacing "r" there. You will get
 + + 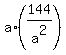 = 26, or = 26, or
 + + 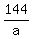 = 26.
Multiply by "a" both sides and simplify
a^2 - 26a + 144 = 0, = 26.
Multiply by "a" both sides and simplify
a^2 - 26a + 144 = 0,
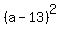 - 169 + 144 = 0 - 169 + 144 = 0
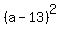 = 25
a - 13 = +/- = 25
a - 13 = +/-  = +/- 5.
Thus two solutions for "a" are a = 13 + 5 = 18 or a = 13 - 5 = 8.
If a = 8, then from (4) r = = +/- 5.
Thus two solutions for "a" are a = 13 + 5 = 18 or a = 13 - 5 = 8.
If a = 8, then from (4) r =  = =  .
If a = 18, then from (4) r = .
If a = 18, then from (4) r = 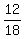 = =  .
In the first case, if a = 8, then the three terms are 8, .
In the first case, if a = 8, then the three terms are 8, 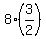 = 12 and = 12 and 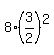 = 18.
In this case, the sum of terms is 8 + 12 + 18 = 38, so this solution does work.
In the second case, if a = 18, then the three terms are 18, = 18.
In this case, the sum of terms is 8 + 12 + 18 = 38, so this solution does work.
In the second case, if a = 18, then the three terms are 18, 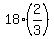 = 12 and = 12 and 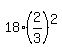 = 8.
In this case, the sum of terms is 18 + 12 + 8 = 38, so this solution does work, too.
ANSWER. The problem has two solution:
a) first term is 18; the common difference is = 8.
In this case, the sum of terms is 18 + 12 + 8 = 38, so this solution does work, too.
ANSWER. The problem has two solution:
a) first term is 18; the common difference is  and the progression is 18, 12, 8.
b) first term is 8; the common difference is and the progression is 18, 12, 8.
b) first term is 8; the common difference is  and the progression is 8, 12, 18. and the progression is 8, 12, 18.
Solved.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The sum of the first three terms in a GP is 38. Their product is 1728. Find the values of the three terms.
My answer were 8 and 18. I want to confirm if it's correct and how will I find the values of the three terms with two solution of a and r
SUM of the 3 terms: 
 ------- eq (i) ------- eq (i)
Product of the 3 terms: 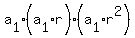 , and so: , and so:  ======> ======> 
 --------- eq (ii) --------- eq (ii)
We then get: 
 ------ Cross-multiplying ------ Cross-multiplying
 ------- Factoring out GCF, 2 ------- Factoring out GCF, 2




3r(2r - 3) - 2(2r - 3) = 0
(3r - 2)(2r - 3) = 0
3r - 2 = 0 OR 2r - 3 = 0
3r = 2 OR 2r = 3




Therefore, if r, or common ratio =  , then , then  or 1st term = 18 or 1st term = 18
In this case, the 3 terms are: 



Therefore, if r, or common ratio =  , then , then  or 1st term = 8 or 1st term = 8
In this case, the 3 terms are: 
|
|
|