|
Question 1155269: A manufacturer of wooden articles produces tables and chairs which require two types of inputs mainly, the being wood and labour. The manufacturer knows that for a table 3 units of wood and 1 unit of labour are required while for a chair they are 2 units each. The profit from each table is 20 USD while it is 16 USD for each chair. The total available resources for the manufacture are 150 units of wood and 75 units of labour. The minimum demand for chairs is 10 and the minimum demand for tables is 8. The manufacturer wants to maximize his profit by distributing his resources for tables and chairs. Formulate the problem mathematically.
Found 3 solutions by Theo, greenestamps, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this is a linear programming type problem.
x represents the number of tables.
y represents the number of chair.
the objective function is profit = 20 * x + 16 * y
the constraints are:
3 * x + 2 * y <= 150
that's 3 units of wood for * the number of tables plus 2 units of wood * the number of chairs.
x + 2 * y <= 75
that's 1 unit of labor * the number of tables plus 2 units of labor * the number of chair.
x >= 8
that's because the minimum number of tables is 8.
y >= 10
that's because the minimum number of chairs is 10.
x,y >= 0
that's because the minimum number of chair or tables is equal to 0, i.e. it can't be negative.
if you drew a table, it might make it easier to understand what's going on.
the table might look like this.
tables chairs total
number of x y
units of wood 3 2 <= 150
units of labor 1 2 <= 75
demand >= 8 >= 10
profit 20 16
to summarize the formulas required, you get:
objective function is profit = 20x + 16y
units of wood constraint is 3x + 2y <= 150
labor constraint is x + 2y <= 75
demand constraint is x >= 8 and y >= 10
profit = 20x + 16y
no negative units is x >= 0 and y >= 0
this requirement is redundant in this problem because you already have x >= 8 and y >= 10 which eliminates the need for x >= 0 and y >= 0. this will not always be the case, depending on the problem.
there is a simplex method tool that can be used to solve a problem such as this.
that tool can be found at
the output of that tool looks like this.

the maximum profit is 1050.
37.5 units of wood are used and 18.75 units of labor are used.
the graphical solution confirms the answer.
it looks like this.

with the desmos.com calculator, you plot the opposite of your constraints.
the area of the graph that is not shaded is you region of feasibility.
the corner points of that region are where your maximum profit will be.
you evaluate your profit function at each corner point.
for example, when x = 37.5 and y = 18.75, your profit is 20 * 37.5 + 16 * 18.75 = 1050.
the simplex tool also contains a tutorial on how to manually develop a solution using the simplex method.
the graphing method can be used with two variables.
anything more than that uses different methods that are not graphical, such as the simplex method and others.
excel can also be used but it's more difficult to set up than the simplex method tool i showed you.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Note that the problem says "Formulate the problem mathematically."
It does not say anything about solving the problem....
Assuming the problem IS supposed to be solved, here is a shortcut you can use for most problems like this where there are constraints on only two variables.
(1) Plot the two major constraint boundary lines.
(2) Determine the slope of each boundary line and the slope of the constraint line.
The point of the feasibility region where the objective function is maximized is where a line with the slope of the objective function just touches the feasibility region. That point can be determine by comparing the three slopes.
For this problem, the major constraint boundary lines are
(1)  --> --> 
(2)  --> --> 
The objective function is  which has a slope of -5/4. which has a slope of -5/4.
Because -5/4 is between -1/2 and -3/2, the point where the objective function is maximized is where the two major constraint lines intersect.
So there is no need to evaluate the objective function at any point other than that point of intersection.
Algebra shows the point of intersection to be (x,y) = (37.5,18.75).
Note the non-integer values are probably okay if we consider the given data to be average daily production -- so that, for example, the maximum profit over 4 days is if 150 tables and 75 chairs are produced.
Note also that we need to make sure the solution we found satisfies the other constraints that, up to this point, we have ignored.
They do, so we have our answer.
ANSWER: 37.5 tables and 18.75 chairs (per day?) for a maximum (daily) profit of 20(37.5)+16(18.75) = 750+300 = 1050 USD.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Mathematical frame for this minimization problem is as it is presented in the post by @Theo
x = # of tables;
y = # of chairs;
Objective function P(x,y) = 20x + 16y
Constraints are
3x + 2y <= 150
x + 2y <= 75
x >= 8, y >= 10.
+--------------------------------------------------+
| B U T B U T B U T B U T B U T B U T |
+--------------------------------------------------+
But it is VERY specific / special maximization problem.
According to the context, it REQUIRES the solution x and y in INTEGER numbers.
Again : in integer numbers --- not in real.
So, it is Linear Programming problem in integer numbers.
It is very special/specific problem, and it requires ADEQUATE METHODS of solution.
Again : this very special/specific problem requires ADEQUATE METHODS of solution, different from that
what are used in continuum minimization problems.
Look into the post by @Theo: you see there the grid of points in the feasibility quadrilateral.
Our task in this case is to find the maximal solution ON THIS GRID (!)
ON THIS GRID only (!) --- it is the specific of this problem.
What you may find in the continuum model ---- IS NOT THE SOLUTION in integer numbers
and is not the solution to the problem as it is posed.
Now. In the Internet, you may find online solvers for the continuum minimax problems.
One of them is the solver used by @Theo. But, as I just explained, it is not an adequate tool in our specific case.
UNFORTUNATELY, in the Internet you will not find online (free of charge) solver for minimax problems with integer solutions.
(at least, I did not find them, really working, although I spent hours for this search).
But I am a mathematician according to my basic education, and I was a computer programmer-analyst in my past life.
My life experience touched me finding an exit from any complicated situation to REALLY SOLVE a problem.
This time I decided to use Excel to get the solution.
The major idea was that the solution requires to analyze only FINITE set of grid points.
So, I created Excel spreadsheet and quickly got the solution.
This spreadsheet (the Table) is presented below.
First column (called x) is the number of tables. It goes from 8 (see constraint for x) to 44.
(this magician number 44 came from @Theo solution),
Next column (called y1) is  = =  .
Next column (called y1_int) is integer part of values of y1.
Next column (called y2) is .
Next column (called y1_int) is integer part of values of y1.
Next column (called y2) is  = = 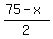 .
Next column (called y2_int) is integer part of values of y2.
Next column (called min(y1_int,y2_int) is for minimum ( .
Next column (called y2_int) is integer part of values of y2.
Next column (called min(y1_int,y2_int) is for minimum (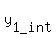 , ,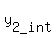 ).
Finally, the last column is the Profit function, calculated on the grid.
As you should understand from my description, I consider the set of integer points of the grid,
belonging to the feasibility quadrilateral and CLOSEST to the boundary lines.
x y1 y1_int y2 y2_int min P=20x+16y
(y1_int,y2_int)
8 63.0 63 33.5 33 33 688
9 61.5 61 33.0 33 33 708
10 60.0 60 32.5 32 32 712
11 58.5 58 32.0 32 32 732
12 57.0 57 31.5 31 31 736
13 55.5 55 31.0 31 31 756
14 54.0 54 30.5 30 30 760
15 52.5 52 30.0 30 30 780
16 51.0 51 29.5 29 29 784
17 49.5 49 29.0 29 29 804
18 48.0 48 28.5 28 28 808
19 46.5 46 28.0 28 28 828
20 45.0 45 27.5 27 27 832
21 43.5 43 27.0 27 27 852
22 42.0 42 26.5 26 26 856
23 40.5 40 26.0 26 26 876
24 39.0 39 25.5 25 25 880
25 37.5 37 25.0 25 25 900
26 36.0 36 24.5 24 24 904
27 34.5 34 24.0 24 24 924
28 33.0 33 23.5 23 23 928
29 31.5 31 23.0 23 23 948
30 30.0 30 22.5 22 22 952
31 28.5 28 22.0 22 22 972
32 27.0 27 21.5 21 21 976
33 25.5 25 21.0 21 21 996
34 24.0 24 20.5 20 20 1000
35 22.5 22 20.0 20 20 1020
36 21.0 21 19.5 19 19 1024
37 19.5 19 19.0 19 19 1044
38 18.0 18 18.5 18 18 1048 (*)<<<---===
39 16.5 16 18.0 18 16 1036
40 15.0 15 17.5 17 15 1040
41 13.5 13 17.0 17 13 1028
42 12.0 12 16.5 16 12 1032
43 10.5 10 16.0 16 10 1020
44 9.0 9 15.5 15 9 1024
1048 <<<---=== MAX
Generating this spreadsheet is very easy: You simply move from on column to the other, from left to right.
Its creation was faster than your reading of my post, and MUCH more fast than my writing of this post.
When the last column is ready and is just filled with numbers, Excel allows to find the maximum in this column quickly.
This row with the solution is marked in my table by this sign (*)<<<---===.
So the problem is just solved, and the
ANSWER is 38 tables and 18 chairs with the maximum profit of 1048 dollars. ).
Finally, the last column is the Profit function, calculated on the grid.
As you should understand from my description, I consider the set of integer points of the grid,
belonging to the feasibility quadrilateral and CLOSEST to the boundary lines.
x y1 y1_int y2 y2_int min P=20x+16y
(y1_int,y2_int)
8 63.0 63 33.5 33 33 688
9 61.5 61 33.0 33 33 708
10 60.0 60 32.5 32 32 712
11 58.5 58 32.0 32 32 732
12 57.0 57 31.5 31 31 736
13 55.5 55 31.0 31 31 756
14 54.0 54 30.5 30 30 760
15 52.5 52 30.0 30 30 780
16 51.0 51 29.5 29 29 784
17 49.5 49 29.0 29 29 804
18 48.0 48 28.5 28 28 808
19 46.5 46 28.0 28 28 828
20 45.0 45 27.5 27 27 832
21 43.5 43 27.0 27 27 852
22 42.0 42 26.5 26 26 856
23 40.5 40 26.0 26 26 876
24 39.0 39 25.5 25 25 880
25 37.5 37 25.0 25 25 900
26 36.0 36 24.5 24 24 904
27 34.5 34 24.0 24 24 924
28 33.0 33 23.5 23 23 928
29 31.5 31 23.0 23 23 948
30 30.0 30 22.5 22 22 952
31 28.5 28 22.0 22 22 972
32 27.0 27 21.5 21 21 976
33 25.5 25 21.0 21 21 996
34 24.0 24 20.5 20 20 1000
35 22.5 22 20.0 20 20 1020
36 21.0 21 19.5 19 19 1024
37 19.5 19 19.0 19 19 1044
38 18.0 18 18.5 18 18 1048 (*)<<<---===
39 16.5 16 18.0 18 16 1036
40 15.0 15 17.5 17 15 1040
41 13.5 13 17.0 17 13 1028
42 12.0 12 16.5 16 12 1032
43 10.5 10 16.0 16 10 1020
44 9.0 9 15.5 15 9 1024
1048 <<<---=== MAX
Generating this spreadsheet is very easy: You simply move from on column to the other, from left to right.
Its creation was faster than your reading of my post, and MUCH more fast than my writing of this post.
When the last column is ready and is just filled with numbers, Excel allows to find the maximum in this column quickly.
This row with the solution is marked in my table by this sign (*)<<<---===.
So the problem is just solved, and the
ANSWER is 38 tables and 18 chairs with the maximum profit of 1048 dollars.
The solution is completed
----------------
The post-solution note.
Eventually, the solution is close to the continuum solution, found by @Theo.
But do not attach importance to this fact:
in integer mode solution, the optimum point can be far enough from the continuum solution.
Just D O N E.
|
|
|
| |