SOLUTION: There are four numbers in an Arithmetic Progression. The sum of the two extremes is 8, and the product of the middle two numbers is 15. What are the numbers?

Let x be the very central point for the given 4 terms of the AP.


In other words, let x be the average of the 4 terms of the AP


    x = .


Next, let d be the common difference of the AP.


Our goal is to find "x" and "d".


It is clear that 

     = x - 1.5d;

     = x - 0.5d;

     = x + 0.5d;

     = x + 1.5d.



Therefore,   +  = 2x.


It implies  2x = 8, and hence  x = 4.



Also,   = 15.


It implies  (x-0.5d)*(x+0.5d) = 15,  or

            x^2 - 0.25d^2 = 15.


Substitute here x= 4 to get

            0.25d^2 = 4^2 - 15 = 16 - 15 = 1.


Thus  d^2 = 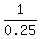 = 4;  hence,  d =  = +/- 2.


The problem is just solved. We know the central point x = 4  and the common difference d = +/-2.


If d = 2, then   = 4-1.5*2 = 1;   = 1+2 = 3;   = 3+2 = 5,  and   = 5 + 2 = 7.


If d = -2,  then we have the same sequence in the REVERSED order:   = 7;   = 5;   = 3  and   = 1.