.
Given 2, 5, 8 as a sequence. Prove that none of the terms 
 is a perfect square
is a perfect square
~~~~~~~~~~~~~~~~~~
Please notice how I edited your post to create an adequate meaning.
This sequence is an arithmetic progression with the common difference of 3 and the first term 2.
When dividing by 3, all the terms of the progression give the remainder of 2.
No one perfect square gives the remainder 2 when is dividing by 3.
Indeed, let's consider an arbitrary square  of an integer number "n".
If n is multiple of 3, n = 3k, then
of an integer number "n".
If n is multiple of 3, n = 3k, then  is a multiple of 9; hence, it is a multiple of 3, giving the remainder 0 whin divided by 3.
If n = 3k+1, then
is a multiple of 9; hence, it is a multiple of 3, giving the remainder 0 whin divided by 3.
If n = 3k+1, then  =
= 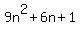 , giving the remainder 1, when divided by 3.
If n = 3k+2, then
, giving the remainder 1, when divided by 3.
If n = 3k+2, then  =
= 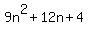 , giving the remainder 1, when divided by 3.
It proves the statement.
, giving the remainder 1, when divided by 3.
It proves the statement.