SOLUTION: find sum to infinity for following sequence 1 , 2/3 , 3/9 , 4/27 , 5/81 , ....

 1/1 + 2/3 + 3/9 + 4/27 + 5/81 +  ...

The sequence of numerators is 1, 2, 3, 4, 5. ..., which has nth term n.

The sequence of denominators is 1, 3, 9, 27, 81, ..., which has nth term 3n.

So the series we want has nth term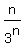 

We want the infinite sum 

We start with the geometric series formula



Substitute a=1



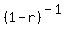Differentiate both sides with respect to r:





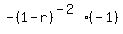
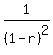Substitute r=1/3



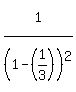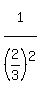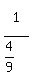We need to make the coefficient match the exponent. 
So we write the first n as n-1+1 and then as (n-1)+1



Distribute



Distribute the sum:



We change the limits, so that n-1 will be a single letter.
We want n-1 = k, so we substitute n = k+1 





Now we can go back to our original notation by changing k to n:



But we now have n starting at -1.  But we want n to start at 0, so we write
out the first term separately, then the rest of the sum will begin at n=0



Simplifying, the terms we wrote separately are -3 and 3, so they cancel:



The second sum is an infinite geometric series with a=1 an r=1/3 so we use
the sum formula for an infinite geometric series and get 

       

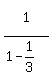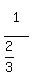So we substitute 3/2 for the second sum and have:



and solve for the sum, which is what we want:



Edwin