Question 1144114: if k+1,2k-1, 3k+1,are three consecutive terms of a geometric progression, find the possible values of the common ratio?
please help me to show the
workings in full.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If k+1, 2k-1, 3k+1 are three consecutive terms of a geometric progression, then
the ratio 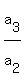 is equal to the ratio is equal to the ratio  ,
by the definition of a geometric progression.
Hence, ,
by the definition of a geometric progression.
Hence,
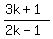 = = 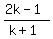 .
It implies
(3k+1)*(k+1) = (2k-1)^2
3k^2 + k + 3k + 1 = 4k^2 - 4k + 1
k^2 - 8k = 0
k*(k-8) = 0
which has two roots k= 0 and k= 8.
If k= 0, then the first and the second terms of the GP are k+1 = 1 and 2k-1 = -1, so the common ratio is .
It implies
(3k+1)*(k+1) = (2k-1)^2
3k^2 + k + 3k + 1 = 4k^2 - 4k + 1
k^2 - 8k = 0
k*(k-8) = 0
which has two roots k= 0 and k= 8.
If k= 0, then the first and the second terms of the GP are k+1 = 1 and 2k-1 = -1, so the common ratio is 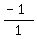 = -1.
If k= 8, then the first and the second terms of the GP are k+1 = 9 and 2k-1 = 15, so the common ratio is = -1.
If k= 8, then the first and the second terms of the GP are k+1 = 9 and 2k-1 = 15, so the common ratio is  = =  .
ANSWER. Under given conditions, the common ratio may have one of the two values -1 and/or .
ANSWER. Under given conditions, the common ratio may have one of the two values -1 and/or  . .
Solved (with a complete explanation).
|
|
|