Question 1143488: if a, b, c are in hp show that 1/a + 1/b+c, 1/b + 1/(c+a), 1/c + 1/(a+b) are
also in hp.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Proposition to prove:
if a, b, c are in hp show that 1/a + 1/(b+c), 1/b + 1/(c+a), 1/c + 1/(a+b) are
also in hp.
Two things we must know
1. Three terms p,q,r are in hp if and only if their reciprocals
1/p, 1/q, 1/r are in ap.
2. Three terms u,v,w are in ap if and only if v-u = w-v
if a, b, c are in hp
That is true if and only if
1/a, 1/b, 1/c are in ap.
That is true if and only if
(1) 
1/a + 1/(b+c), 1/b + 1/(c+a), 1/c + 1/(a+b) are also in hp
That will be true true if and only if after getting LCD's, we can show that:
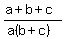 , , 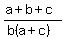 , and , and 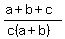 are in hp. That will be true if and only if
are in hp. That will be true if and only if
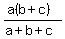 , , 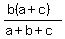 , and , and 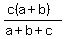 are in ap.
They have the same denominators so they will be in ap if and only if their
numerators are in ap. That will be true if and only if
are in ap.
They have the same denominators so they will be in ap if and only if their
numerators are in ap. That will be true if and only if
 That will be true if and only if
That will be true if and only if
 That will be true if and only if
That will be true if and only if
 That will be true if and only if we can divide through by abc
and this will be true:
That will be true if and only if we can divide through by abc
and this will be true:
 That will be true if and only if we can cancel and get
That will be true if and only if we can cancel and get
 That will be true if and only if we multiply through by -1, and get
That will be true if and only if we multiply through by -1, and get
 That will be true if and only if we can reverse the terms and get
That will be true if and only if we can reverse the terms and get
 And we have that that is true in equation (1) above. So the proposition is
proved.
Edwin
And we have that that is true in equation (1) above. So the proposition is
proved.
Edwin
|
|
|