Question 1140702: t is an even number in the series 1/t + 3/t + 5/t +.......+ t-1/t
(1) Determine the number of terms in the series in terms of t.
(Determine the sum of the series in terms of t.
(3) Hence or otherwise evaluate :
(1/4 + 3/4) + (1/6 + 3/6 + 5/6) + (1/8 + 3/8 + 5/8 +7/8)+.....+ (1/50 + 3/50 + 5/50)+....+(49/50)
Can I get help please
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The series is arithmetic, with a common difference of 2/t.
(1) To find the number of terms in an arithmetic series...
find the difference between the last and first terms;
divide by the common difference; and
add 1.




ANSWER (1): The number of terms in the series is t/2.
(2) The sum of the terms of any series is the number of terms, multiplied by the average of all the terms; since this sequence is arithmetic, that means the sum is the number of terms, multiplied by the average of the first and last terms.
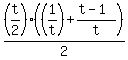
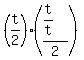

ANSWER: (2): The sum of the terms in the series is t/4.
(3) The terms in this series are all of the form in the above discussion. The values of t in the terms of this series are 4, 6, 8, ..., and 50. So the sum of this series, using the result in (2), is
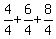 ... + ... + 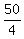
This is again an arithmetic series; the sum is number of terms, multiplied by the average of the first and last:

|
|
|