Given: The first 3 first differences for a quadratic sequence are 1, 3, and 5.
?? ?? ?? ?? <-- the sequence
1 3 5 <-- first differences
The second differences are all 2, confirming that the sequence is quadratic.
?? ?? ?? ?? <-- the sequence
1 3 5 <-- first differences
2 2 <-- second differences
To find subsequent terms in the sequence, we can continue the constant row of second differences and work back up the array.
?? ?? ?? ?? ?? ?? ?? ?? ?? ... <-- the sequence
1 3 5 7 9 11 13 15 ... <-- first differences
2 2 2 2 2 2 2 ... <-- second differences
Knowing that the 7th term is 35, we can use the first differences to to find earlier (and later) terms in the sequence.
-1 0 3 8 15 24 35 48 63 ... <-- the sequence
1 3 5 7 9 11 13 15 ... <-- first differences
2 2 2 2 2 2 2 ... <-- second differences
ANSWER 1: The 6th and 5th terms of the sequence are 24 and 15.
For the second part of the problem, we need to find the quadratic function 
that produces the terms of the given sequence.
There are many ways to do that. One common way is to make a system of three equations in a, b, and c using three of the terms of the sequence. You could us any three terms; but using the first three terms makes the work easiest.
I won't go that route; you can if you want to (it's good practice!).
I prefer a different path, as follows....
The leading coefficient of the quadratic function we are looking for is the constant 2nd difference, divided by 2!. Since the constant second difference is 2, the leading coefficient of our function is 1.
So our function is of the form 
. To find the coefficients b and c, compare 
to 
:
t(n): -1 0 3 8 ...
n^2 : 1 4 9 16 ...
t(n)-n^2: -2 -4 -6 -8 ...
From this, we can see that "bn+c" is equal to "-2n". So
ANSWER 2: the n-th term of the sequence is given by the quadratic function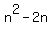 
Note the formula for the n-th term of the sequence is 
. It is easy to use this factored form to verify that the formula produces the correct sequence:
n=1: 1(-1) = -1
n=2: 2(0) = 0
n=3: 3(1) = 3
n=4: 4(2) = 8
n=5: 5(3) = 15
n=6: 6(4) = 24
n=7: 7(5) = 35
...
Looking back at our work, then, we can see that we might have been able to find the formula for the n-th term by discerning this pattern in the numbers in the sequence.
