SOLUTION: The sum of the first three terms of an AP is twenty four and the sum of there square is two hundred twenty four.find first three terms of AP

Algebra ->  Sequences-and-series -> SOLUTION: The sum of the first three terms of an AP is twenty four and the sum of there square is two hundred twenty four.find first three terms of AP      Log On


   

Question 1140594: The sum of the first three terms of an AP is twenty four and the sum of there square is two hundred twenty four.find first three terms of AP
Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
The middle term (the 2-nd term) is one third of the sum, i.e. 24/3 = 8.


The first and the third terms then are  (8-d) and (8+d), where "d" is the common difference.


Then for "d" you have this equation


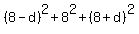%288-d%29%5E2+%2B+8%5E2+%2B+%288%2Bd%29%5E2 = 224.


Simplify and solve for d.


64 - 16d + d^2 + 64 + 64 + 16d + d^2 = 224


2d^2 = 224 - 64 - 64 - 64


2d^2 = 32  ====>  d^2 = 32/2 = 16  ====>  d = +/- 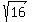sqrt%2816%29 = +/- 4.


So, there are two such progressions:  one is for d = 4,  and the three terms are 4, 8 and 12.


The other is for d = -4, and the three terms are the same in the reversed order  12, 8 and 4.

Solved.