SOLUTION: Find three numbers in arithmetic progression whose sum and product are six and six respectively

First of all, the answer is OBVIOUS:  the three terms are 1, 2 and 3.


The reversed order 3, 2 and 1 works, too.


The solution is OBVIOUS, too.


First step is to notice that the middle term (the 2-nd term) is one third of the sum, i.e. one third of 6, which is 2.


Then the first and the third terms are  (2+d)  and  (2-d), where "d" is the common difference.


From it, you have for the product of the three terms


    (2-d)*2*(2+d) = 6,   which implies

     4 - d^2 = 6/2 = 3,

     d^2 = 4-3 = 1,   hence

     d = +/- 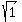 = +/- 1,


which gives the answer.