Question 1138736: sequence50,15,40,59
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
sequence  , , , , , ,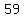
first find differences to see what formula you need
 ....... ....... ....... ....... ....... .......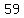
..... ....... ....... ....... .......
........... ....... .......
................. -> -> difference->you need difference->you need
 degree function degree function

use given terms, set up system of four equations
 , , 

 ........eq.1 ........eq.1
 , , 

 .......eq.2 .......eq.2
 , , 

 .......eq.3 .......eq.3
 , , 

 .......eq.4 .......eq.4
solve the system:
 ........eq.1 ........eq.1
 .......eq.2 .......eq.2
 .......eq.3 .......eq.3
 .......eq.4 .......eq.4
------------------------------------------
Solve the system of 4 equations using your favorite method.
In this example, the results are:
 , ,  , ,  , , 
and your formula is:

|
|
|