|
Question 1138580: Find the sum of the series, if it converges. Otherwise, enter DNE.
sum from n to infinity of: 3/(n(n+2))
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the sum of the series, if it converges. Otherwise, enter DNE.
sum from n to infinity of: 3/(n(n+2))
~~~~~~~~~~~~~~~~~~~~~~~~
The problem formulation, as it is presented in the post, is INCORRECT.
The correct formulation, after my editing, is below:
Find the sum of the series { sum over n from 1 to infinity of  }. }.
Solution
Use the identity
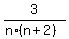 = = 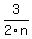 - - 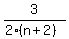 which you can easily prove by writing the right hand side with the common denominator.
It will give you
{ sum from n to infinity of
which you can easily prove by writing the right hand side with the common denominator.
It will give you
{ sum from n to infinity of  } =
= } =
=  - -  +
+ +
+  - - 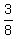 +
+ +
+  - -  +
+ +
+ 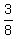 - - 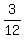 +
+ +
+  - -  +
+ . . . and so on . . .
From this writing, yo can see that in the (infinite) sum all the terms cancel each other, and only two very first terms survive.
These terms are +
+ . . . and so on . . .
From this writing, yo can see that in the (infinite) sum all the terms cancel each other, and only two very first terms survive.
These terms are  + +  , so the series does converge and the sum from 1 to infinity is equal to , so the series does converge and the sum from 1 to infinity is equal to
 + +  = =  + +  = =  = =   = 2.25. ANSWER
CHECK.
n = 2.25. ANSWER
CHECK.
n 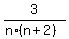 Sum
of the terms
in column 2
1 1.0000 1.0000
2 0.3750 1.3750
3 0.2000 1.5750
4 0.1250 1.7000
5 0.0857 1.7857
6 0.0625 1.8482
7 0.0476 1.8958
8 0.0375 1.9333
9 0.0303 1.9636
10 0.0250 1.9886
11 0.0210 2.0096
12 0.0179 2.0275
13 0.0154 2.0429
14 0.0134 2.0563
15 0.0118 2.0680
16 0.0104 2.0784
17 0.0093 2.0877
18 0.0083 2.0961
19 0.0075 2.1036
20 0.0068 2.1104
21 0.0062 2.1166
22 0.0057 2.1223
23 0.0052 2.1275
24 0.0048 2.1323
25 0.0044 2.1368
26 0.0041 2.1409
27 0.0038 2.1447
28 0.0036 2.1483
29 0.0033 2.1516
30 0.0031 2.1547
31 0.0029 2.1577
32 0.0028 2.1604
33 0.0026 2.1630
34 0.0025 2.1655
35 0.0023 2.1678
36 0.0022 2.1700
37 0.0021 2.1721
38 0.0020 2.1740
39 0.0019 2.1759
40 0.0018 2.1777
41 0.0017 2.1794
42 0.0016 2.1810
43 0.0016 2.1826
44 0.0015 2.1841
45 0.0014 2.1855
46 0.0014 2.1868
47 0.0013 2.1881
48 0.0013 2.1894
49 0.0012 2.1906
50 0.0012 2.1917
51 0.0011 2.1929
52 0.0011 2.1939
53 0.0010 2.1949
54 0.0010 2.1959
55 0.0010 2.1969
56 0.0009 2.1978
57 0.0009 2.1987
58 0.0009 2.1996
59 0.0008 2.2004
60 0.0008 2.2012
61 0.0008 2.2020
62 0.0008 2.2028
63 0.0007 2.2035
64 0.0007 2.2042
65 0.0007 2.2049
66 0.0007 2.2056
67 0.0006 2.2062
68 0.0006 2.2068
69 0.0006 2.2074
70 0.0006 2.2080
71 0.0006 2.2086
72 0.0006 2.2092
73 0.0005 2.2097
74 0.0005 2.2103
75 0.0005 2.2108
76 0.0005 2.2113
77 0.0005 2.2118
78 0.0005 2.2123
79 0.0005 2.2127
80 0.0005 2.2132
81 0.0004 2.2136
82 0.0004 2.2141
83 0.0004 2.2145
84 0.0004 2.2149
85 0.0004 2.2153
86 0.0004 2.2157
87 0.0004 2.2161
88 0.0004 2.2165
89 0.0004 2.2168
90 0.0004 2.2172
91 0.0004 2.2176
92 0.0003 2.2179
93 0.0003 2.2183
94 0.0003 2.2186
95 0.0003 2.2189
96 0.0003 2.2192
97 0.0003 2.2195
98 0.0003 2.2198
99 0.0003 2.2201
100 0.0003 2.2204 Sum
of the terms
in column 2
1 1.0000 1.0000
2 0.3750 1.3750
3 0.2000 1.5750
4 0.1250 1.7000
5 0.0857 1.7857
6 0.0625 1.8482
7 0.0476 1.8958
8 0.0375 1.9333
9 0.0303 1.9636
10 0.0250 1.9886
11 0.0210 2.0096
12 0.0179 2.0275
13 0.0154 2.0429
14 0.0134 2.0563
15 0.0118 2.0680
16 0.0104 2.0784
17 0.0093 2.0877
18 0.0083 2.0961
19 0.0075 2.1036
20 0.0068 2.1104
21 0.0062 2.1166
22 0.0057 2.1223
23 0.0052 2.1275
24 0.0048 2.1323
25 0.0044 2.1368
26 0.0041 2.1409
27 0.0038 2.1447
28 0.0036 2.1483
29 0.0033 2.1516
30 0.0031 2.1547
31 0.0029 2.1577
32 0.0028 2.1604
33 0.0026 2.1630
34 0.0025 2.1655
35 0.0023 2.1678
36 0.0022 2.1700
37 0.0021 2.1721
38 0.0020 2.1740
39 0.0019 2.1759
40 0.0018 2.1777
41 0.0017 2.1794
42 0.0016 2.1810
43 0.0016 2.1826
44 0.0015 2.1841
45 0.0014 2.1855
46 0.0014 2.1868
47 0.0013 2.1881
48 0.0013 2.1894
49 0.0012 2.1906
50 0.0012 2.1917
51 0.0011 2.1929
52 0.0011 2.1939
53 0.0010 2.1949
54 0.0010 2.1959
55 0.0010 2.1969
56 0.0009 2.1978
57 0.0009 2.1987
58 0.0009 2.1996
59 0.0008 2.2004
60 0.0008 2.2012
61 0.0008 2.2020
62 0.0008 2.2028
63 0.0007 2.2035
64 0.0007 2.2042
65 0.0007 2.2049
66 0.0007 2.2056
67 0.0006 2.2062
68 0.0006 2.2068
69 0.0006 2.2074
70 0.0006 2.2080
71 0.0006 2.2086
72 0.0006 2.2092
73 0.0005 2.2097
74 0.0005 2.2103
75 0.0005 2.2108
76 0.0005 2.2113
77 0.0005 2.2118
78 0.0005 2.2123
79 0.0005 2.2127
80 0.0005 2.2132
81 0.0004 2.2136
82 0.0004 2.2141
83 0.0004 2.2145
84 0.0004 2.2149
85 0.0004 2.2153
86 0.0004 2.2157
87 0.0004 2.2161
88 0.0004 2.2165
89 0.0004 2.2168
90 0.0004 2.2172
91 0.0004 2.2176
92 0.0003 2.2179
93 0.0003 2.2183
94 0.0003 2.2186
95 0.0003 2.2189
96 0.0003 2.2192
97 0.0003 2.2195
98 0.0003 2.2198
99 0.0003 2.2201
100 0.0003 2.2204
Solved.
This trick, which I used in my solution, is very well known.
See the lesson
- Calculations with fractions
in this site.
|
|
|
| |