Question 1138563: 1/2,2/5,1,
What's the sixth term of sequence?
Found 3 solutions by greenestamps, ikleyn, MathLover1:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It is impossible to know the "right" answer to any problem like this.
You can put any numbers you want for the subsequent terms of the sequence, so of course the 6th term could be anything.
Presumably there is a pattern to the given numbers which produces a particular 6th term.
However, there are almost certainly other very different patterns that produce the given sequence of numbers and will produce different 6th terms.
If you are so inclined, spend a few minutes at the very most to try to find a logical pattern that produces the given first three numbers in the sequence.
But realize that, even if you DO find a nice pattern that works, it might not be the "right" pattern, and your logically obtained answer will be "wrong".
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I have a grandioze commercial idea ! ! !
Create the (advertizing-funded) site / forum "What is the next number.com" and post and collect there such problems.
Very soon you will become a millionaire !
You will be very happy ! ! We will be happy, too !
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
first find differences to see what formula we need
 ........ ........ .... .... .... ....
...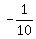 ...... ......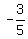 , .... , ....
............ ..........2nd difference tells us we have ..........2nd difference tells us we have  sequence, so we need sequence, so we need

now use given terms to find  , , and and 
 => =>

 .......eq.1 .......eq.1
 => =>


 .........eq.2 .........eq.2
 => =>

 ......eq.3 ......eq.3
subtract eq.1 from eq.3 :

 ......solve for ......solve for 


 ...........eq.1a ...........eq.1a
plug in eq.2
 .........eq.2 .........eq.2

 .........solve for .........solve for 



 ............eq.2a ............eq.2a
go to eq.1, plug in  and and  from eq.1a and eq.2a from eq.1a and eq.2a
 .......eq.1......solve for .......eq.1......solve for 






go to  ...........eq.1a, plug in ...........eq.1a, plug in 



go to
 ............eq.2a, plug in ............eq.2a, plug in 



=> , , , , 
=> nth term formula is: 
now, you need to find the sixth term of sequence,  , where , where 







|
|
|