Question 1135971: The sum of the 1st and 2nd term of an A.P is 4 and the 10th term is 19.find the sum of the 5th and 6th term
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From the condition, you have these two equations
 + +  = 4 = 4
 + 9*d = 19.
Or, in the equivalent form,
2a + d = 4, (1)
a + 9d = 19. (2)
From eq(1), express d = 4 - 2a and substitute it into eq(2). You will get
a + 9*(4-2a) = 19,
a + 36 - 18a = 19,
-17a = 19 - 36 = -17 ===========> a = + 9*d = 19.
Or, in the equivalent form,
2a + d = 4, (1)
a + 9d = 19. (2)
From eq(1), express d = 4 - 2a and substitute it into eq(2). You will get
a + 9*(4-2a) = 19,
a + 36 - 18a = 19,
-17a = 19 - 36 = -17 ===========> a = 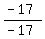 = 1.
Then from eq(1), d = 4 - 2*1 = 2.
So, the arithmetic progression has the first term 1 and the common difference 2.
The progression is 1, 3, 5, 7, 9, 11, 13 . . .
The 5-th term is 1 + 4*2 = 9 and the 6-th term is 1 + 5*2 = 11;
their sum is 9 + 11 = 20. ANSWER = 1.
Then from eq(1), d = 4 - 2*1 = 2.
So, the arithmetic progression has the first term 1 and the common difference 2.
The progression is 1, 3, 5, 7, 9, 11, 13 . . .
The 5-th term is 1 + 4*2 = 9 and the 6-th term is 1 + 5*2 = 11;
their sum is 9 + 11 = 20. ANSWER
Solved.
/\/\/\/\/\/\/\/\/\/\/
On this problem (in its earlier version), I wrote my post under the link
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1135935.html
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1135935.html
but obtained an "UNSATISFIED" response from the visitor - absolutely UNJUSTLY (instead of his (or her) deepest "THANKS").
(After my explanation to the visitor that he (or she) absolutely incorrectly formulated the problem,
and after my explanation on how it should be done correctly - and after my solution.
I did not forget it . . . )
|
|
|