Question 1133165: 8;18;30:44
Calculate the nth term
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
 , , , -> find differences first
.............................
..... ......... ...........
The pattern goes +, +, +, ...
Since the second difference is always + , the nth term must involve  .
So let's say the nth number in the sequence =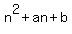 
To find  , you can substitute in  , i.e. what is the "zeroth" number in the sequence? In other words, what number would have come before ?
This number must have been  , in order to continue the pattern of +, +, +, +, ...
So we now know the nth number =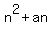 
Now just plug in any other value we know, to find the value of . For example, using the first number in the sequence ( ), we get:
Therefore the nth term in this sequence is: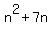 
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
I will copy the very good response from tutor @MathLover1 and expand on it a bit....
,,, -> find differences first
----------------------------------------------------------------
I revised and added some to this display....
8 18 30 44 (the given sequence)
10 12 14 (the "first" differences -- differences between successive terms)
2 2 (the "second differences -- differences between successive first differences)
--------------------------------------------------------
The pattern goes +, +, +, ...
Since the second difference is always +, the nth term must involve .
------------------------------------------------------------------
I'll add a lot here, assuming you are not familiar with what she says there.
In this problem, the second differences are a constant 2, which is 2!. In general, if the second differences are a constant 2k, then the sequence can be produced by a polynomial with leading term kx^2. So, for example, if you have a similar problem where the constant second differences are 8, the sequence can be produced by a polynomial with leading term 4x^2.
The idea continues for polynomials of higher degrees:
If the polynomial has leading term kx^3, then the constant 3rd differences will be 6k (where 6 = 3!).
If the polynomial has leading term kx^4, then the constant 4th differences will be 24k (where 24 = 4!).
And so on....
-------------------------------------------------------------
So let's say the nth number in the sequence =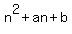
To find , you can substitute in , i.e. what is the "zeroth" number in the sequence? In other words, what number would have come before ?
This number must have been , in order to continue the pattern of +, +, +, +, ...
So we now know the nth number =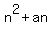
Now just plug in any other value we know, to find the value of. For example, using the first number in the sequence (), we get:
Therefore the nth term in this sequence is: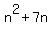
|
|
|
