SOLUTION: The sum of three numbers in Ap is 39 and the sum of their product is 2184.find the number

Click here to see ALL problems on Sequences-and-series

Question 1132438: The sum of three numbers in Ap is 39 and the sum of their product is 2184.find the number
Found 3 solutions by Alan3354, ikleyn, greenestamps:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
Define "sum of their product"
----------------
It's not our (the tutors') responsibility to figure out what you might have meant.
If you can't state the problem clearly, you need to work on that and then, after achieving that, you can work on math.

Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website!
.

                        The condition is FATALLY UNCOMPLETED.

                        It MUST be edited to make sense.

                        My editing is below:

The sum of three CONSECUTIVE numbers in Ap is 39 and the sum of their products is 2184. Find the numbers.

Solution

Let x, y, z be the three consecutive terms of the AP. Then x = y-d, z = y+d, where "d" is the common difference of the AP. Hence, the sum of the three terms is x + y + z = (y-d) + y + (y+d) = 3y. Since the sum is given (39), the middle term of the AP is y = 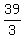= 13. OK, very good. Now we have the second condition related to the sum of the products xy + xz + yz = 2184 = (y-d)*y + (y-d)*(y+d) + y*(y+d) = (y^2 - dy) + (y^2 - d^2) + (y^2 + dy) = 3y^2 - d^2. Hence, 3y^2 - d^2 = 2184. Substitute here y= 13, the value that we found above. You will get 3*13^2 - d^2 = 2184, 3*13^2 - 2184 = d^2 d^2 = 3*169 - 2184 = -1677. At this point, I conclude that the numbers in your post are W R O N G, since the square of a real number CAN NOT BE negative.

D I A G N O S I S.   Your post is good only to be thrown into the GARBAGE BOX.

By posting wrong input data, you simply STOLE my time, which I spent for nothing.

The only positive outcome of my work is preventing other tutors from loosing their valuable time.

============

I'd like to comment the post by @greenestamps.

Dear tutor greenestamps ! A true gentlemen would start his post in such a way: "Thanks to tutor @ikleyn who showed that the original formulation of the problem is incorrect and leads to NOWHERE, saving time for other tutors / (for me, in particular) to try another ways."

Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

The statement of the problem is indeed faulty; but the other tutor who tried to answer the question revised the statement of the problem in a way that made a solution impossible (and the algebra involved in TRYING to solve the problem difficult).

A different correction to the statement of the problem gives a problem that is relatively easy to solve:

The sum of three numbers in Ap is 39 and their product is 2184.find the number

Given that the sum of three numbers in arithmetic progression is 39, the middle number is 13. So the numbers are 13-x, 13, and 13+x.

There are many ways to solve the problem from there. Probably the easiest is to recognize that (13-x)(13)(13+x) is "close" to 13^3; and 13^3 = 2197. That makes it highly likely that x=1; and indeed 12*13*14 = 2184.