Question 1122510: find the sum of each of the following sequences up to n terms.
(a) 8,88,888,...
(b)0.2,0.22,0.222,...
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
find the sum of each of the following sequences up to n terms.
(a) 8, 88, 888, . . .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So, we want to find the sum
R = 8 + 88 + 888 + . . . + 888...8, (1)
where the last number is written using "n" digits of 8.
Consider another sum
T = 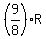 = 9 + 99 + 999 + . . . + 999...9, (2)
where the last number is written using "n" digits of 9.
Add n to T. It is the same as to add "1" to each term of the sum (2). Therefore,
T + n = 10 + 100 + 1000 + . . . + 10^n. (3)
The sum (3) is the sum of the first n terms of the geometric progression with the first term 10 and the common ratio of 10.
So, the sum (3) is equal to
T + n = = 9 + 99 + 999 + . . . + 999...9, (2)
where the last number is written using "n" digits of 9.
Add n to T. It is the same as to add "1" to each term of the sum (2). Therefore,
T + n = 10 + 100 + 1000 + . . . + 10^n. (3)
The sum (3) is the sum of the first n terms of the geometric progression with the first term 10 and the common ratio of 10.
So, the sum (3) is equal to
T + n = 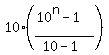 = = 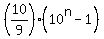 .
Thus you have
T = .
Thus you have
T = 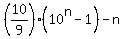 , or , or
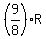 = = 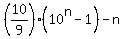 , which implies
R = , which implies
R = 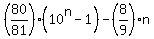 .
It is the final formula and the ANSWER : R = 8 + 88 + 888 + . . . + 888...8 = .
It is the final formula and the ANSWER : R = 8 + 88 + 888 + . . . + 888...8 = 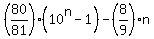 .
Check. Let us take n = 2. Then from one side, R = 8 + 88 = 96.
From the other side, R = .
Check. Let us take n = 2. Then from one side, R = 8 + 88 = 96.
From the other side, R = 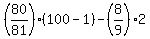 = = 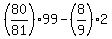 = = 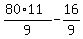 = = 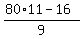 = = 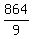 = 88. ! Correct !
Let us take n = 3. Then from one side, R = 8 + 88 + 888 = 984.
From the other side, R = = 88. ! Correct !
Let us take n = 3. Then from one side, R = 8 + 88 + 888 = 984.
From the other side, R =  = =  = = 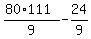 = = 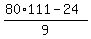 = = 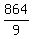 = 984. ! Correct ! = 984. ! Correct !
|
|
|