Question 1121709: The sum of 12 terms of an arithmetic series is 1212. The first term a and the common difference d are both whole numbers. Write down the first three terms of the series
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There is not enough information to get a single answer. There are several arithmetic series that satisfy the given conditions.
The sum of the 12 terms is 1212, so the average is 101. We can think of it as 6 pairs of numbers each with a sum of 202.
So we know the sum of the 1st and 12th numbers is 202; and also that the sum of the 6th and 7th numbers is 202.
That leaves several possible solutions with the common difference and first term both being whole numbers.
(1) The two middle numbers could be 100 and 102; that makes the common difference 2; the first term is 100 minus 5 times the common difference; the last term is 102 plus 5 times the common difference; the series is
90, 92, 94, ..., 100, 102, ..., 112.
(2) The two middle numbers could be 99 and 103; that makes the common difference 4; the first term is 100 minus 5 times the common difference; the last term is 102 plus 5 times the common difference; the series is
79, 83, 87, ..., 99, 103, ..., 123.
And so on. The largest possible whole number common difference, if the first term is also a whole number, is 18; the series is
2, 20, 38, ..., 92, 110, ..., 200.
Since the problem says the common difference is a whole number (instead of a positive integer), you could even have the common difference 0; the series would be
101, 101, 101, ..., 101, 101, ..., 101.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Actually, there are TENS arithmetic progressions satisfying the given conditions.
So the question and the problem, as they formulated, posted and presented, MAKE NO SENSE.
-----------------
Comment from student : Can you also help me out with this last question?
Write down the first three terms of a arithmetic series whos sum is 1212 The series must have a minimum of 13 terms.
The first term and the common difference are integers.
-----------------
My response :
The formula for the sum of the first n terms of an arithmetic progression is
 = =  .
So, in your case it should be .
So, in your case it should be
 = 1212, or = 1212, or 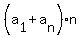 = 2424.
Notice that 2424 = 24*101, and 101 is a prime number.
It means that "n" must divide 101 or must divide some multiple of 101.
Now the first example of such arithmetic progression is THIS:
101 terms, each equal to 12.
It is arithmetic progression consisting of 101 equal terms; each term is equal to 12; the common difference is 0 (zero).
The second example is
202 terms, each equal to 6.
It is arithmetic progression consisting of 202 equal terms; each term is equal to 6; the common difference is 0 (zero).
Having these two examples, you can easily construct other similar examples with the common difference of 0.
I will help you to construct one more example with the non-zero common difference.
51-th term is 12;
50-th term is 11; 52-th term is 13;
49-th term is 10; 53-th term is 14.
. . . and so on . . . . . . . .
1-st term is 12-50 = - 38; 101-th term is 12+50 = 62.
Notice that each pair of the terms in each line has half the sum of 12 (!)
Thus, the progression starts from -38; has the common difference of 1; the last, 101-th term is 62; the sum of the first 101 terms is = 2424.
Notice that 2424 = 24*101, and 101 is a prime number.
It means that "n" must divide 101 or must divide some multiple of 101.
Now the first example of such arithmetic progression is THIS:
101 terms, each equal to 12.
It is arithmetic progression consisting of 101 equal terms; each term is equal to 12; the common difference is 0 (zero).
The second example is
202 terms, each equal to 6.
It is arithmetic progression consisting of 202 equal terms; each term is equal to 6; the common difference is 0 (zero).
Having these two examples, you can easily construct other similar examples with the common difference of 0.
I will help you to construct one more example with the non-zero common difference.
51-th term is 12;
50-th term is 11; 52-th term is 13;
49-th term is 10; 53-th term is 14.
. . . and so on . . . . . . . .
1-st term is 12-50 = - 38; 101-th term is 12+50 = 62.
Notice that each pair of the terms in each line has half the sum of 12 (!)
Thus, the progression starts from -38; has the common difference of 1; the last, 101-th term is 62; the sum of the first 101 terms is
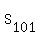 = = 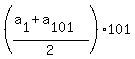 = = 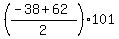 = = 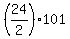 = 12*101 = 1212. = 12*101 = 1212.
Now, if you think carefully on this example, you will be able to construct your own examples with common differences 2, 3, and so on.
-------------------
On arithmetic progressions, there is a bunch of lessons in this site:
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Mathematical induction and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|