Question 1120323: For a geometric series, S2 = 20 and S3= 65. Find the first 3 terms.
Found 3 solutions by solver91311, ikleyn, greenestamps:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From the condition, we have
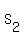 = = 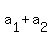 = = 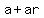 = a*(1+r), (1) = a*(1+r), (1)
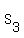 = = 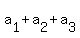 = =  = = 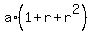 . (2)
Divide (1) by (2). You will get . (2)
Divide (1) by (2). You will get
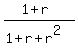 = = 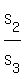 = = 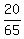 = = 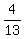 .
or
13(1+r) = 4*(1+r+r^2),
13 + 13r = 4 + 4r + 4r^2
4r^2 -9r - 9 = 0 .
or
13(1+r) = 4*(1+r+r^2),
13 + 13r = 4 + 4r + 4r^2
4r^2 -9r - 9 = 0
 = = 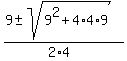 = = 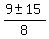 ; ;
 = = 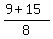 = 3; = 3;  = = 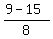 = = 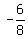 = =  .
Subtract (1) from (2). You will get .
Subtract (1) from (2). You will get
 = = 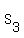 - - 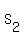 = 65 - 20 = 45 = = 65 - 20 = 45 = 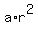 . (*)
Thus we should consider TWO opportunities:
1. If r = 3, then according to (*) . (*)
Thus we should consider TWO opportunities:
1. If r = 3, then according to (*)  = 45 = = 45 = 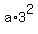 = 9a,
which implies a = 5.
Then = 9a,
which implies a = 5.
Then  = 5, = 5,  = 3*5 = 15 and = 3*5 = 15 and  = 3*15 = 45.
Then = 3*15 = 45.
Then 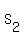 = = 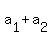 = 5 + 15 = 20 and = 5 + 15 = 20 and 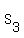 = 5 + 15 + 45 = 65 ! Correct !.
2. If r= = 5 + 15 + 45 = 65 ! Correct !.
2. If r=  , then according (*) a = , then according (*) a = 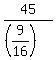 = 5*16 = 80.
Then = 5*16 = 80.
Then  = = 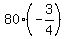 = -60 and = -60 and  = = 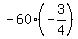 = 45.
In this way, = 45.
In this way, 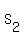 = = 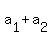 = 80 - 60 = 20
and = 80 - 60 = 20
and 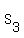 = = 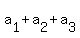 = 80 - 60 + 45 = 65.
So, this opportunity does work, too.
Answer. There are TWO solutions.
One solution is a= 5, r= 3 and the three terms are 5, 15, 45.
Another solution is a= 80, r= = 80 - 60 + 45 = 65.
So, this opportunity does work, too.
Answer. There are TWO solutions.
One solution is a= 5, r= 3 and the three terms are 5, 15, 45.
Another solution is a= 80, r=  and the three terms are 80, -60 and 45. and the three terms are 80, -60 and 45.
Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|