.
The number 1.111111 . . . itself is the sum of the infinite geometric progression with the first term a= 1 and the common ratio 0.1,
so 1.111111 . . . =  =
= 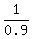 .
Next, the given sum is the sum of the geometric progression with the first term
.
Next, the given sum is the sum of the geometric progression with the first term 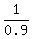 and the common ratio of 0.1,
so this sum is equal to
and the common ratio of 0.1,
so this sum is equal to  =
= 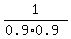 = 1/0.81.
Answer. The sum under the question is equal to
= 1/0.81.
Answer. The sum under the question is equal to 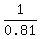 , or
, or 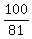 .
.
Solved.