.
We are given 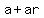 = 90, or
= 90, or 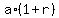 = 90, or a =
= 90, or a = 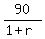 .
We are also given that
.
We are also given that  =
= 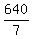 , or a =
, or a =  .
Since left sides of the two last equations are identical, their right sides are equal:
.
Since left sides of the two last equations are identical, their right sides are equal:
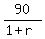 =
=  ,
which implies
90*7 =
,
which implies
90*7 = 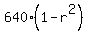 ,
63 =
,
63 = 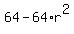 ====>
====> 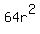 = 64 - 63 = 1 ====>
= 64 - 63 = 1 ====>  =
=  ====> r = +/-
====> r = +/- 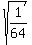 = +/-
= +/-  .
Answer. The two value of the common ratio are +/-
.
Answer. The two value of the common ratio are +/- .
.
Solved.