Question 1110298: The second, fourth and eight terms of an A.p
form the first three consecutive terms of a G.P.
the sum of the third and fifth terms of the A.p is
equal to 20. Find the (a) first 4 terms of the A.p
(b) sum of the first 10 terms of the A.p.
Found 2 solutions by greenestamps, KMST:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
Since the sum of the 3rd and 5th terms of the AP is 20, the 4th term is 10.
If the common difference in the AP is d, then the 2nd term is 10-2d and the 8th term is 10+4d. Since the 2nd, 4th, and 8th terms of the AP form a GP,
 or 
Both values of d satisfy the conditions of the problem; but the AP with d=0 is not very interesting.
With d=2.5 and the 4th term=10, the AP is
2.5, 5, 7.5, 10, 12.5, 15, 17.5, 20, 22.5, 25, ...
Answers:
a) 2.5, 5, 7.5, 10
b) (number of terms) times (average of first and last terms) = 
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! In an A.P. the  term is  , where
 = the first term of the A.P. and
 = the common difference of the A.P.
So, the second, third, fourth, fifth and eight terms are respectively
 ,
 ,
 ,
 and
 .
The sum of the third and fifth terms is
 , which simplifies to
 .
For this problem, that sum is  , so
 <-->  is one of our equations.
As the ratio of consecutive terms in a G.P. is always the same number,
if the second, fourth and eight terms of an A.P.
form the first three consecutive terms of a G.P. ,
then 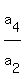  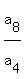 =the common ratio of the G.P.
So,   ,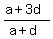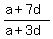
  ,
  ,
  ,
 ,
 ,
 .
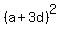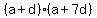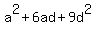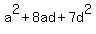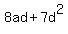Now, we have
 -->  -->  -->  -->  .
(a) Knowing the first term, , and the common difference, ,
we can write any terms of the A.P.
The first 4 terms are
 .
(b) You may have been taught a "formula" for the sum the first  terms of an A.P.
that could be  or something like that.
If a teacher likes to see formulas,
it is a good idea to write the formula the teacher prefers.
Using that formula, the sum of the first 10 terms calculates as
      .
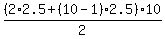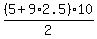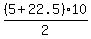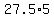I do not memorize formulas, but I remember that
the average of a number of consecutive terms of an A.P. is the average of the first and last of those terms.
I can easily list the second , fourth, sixth, eighth, and ten terms as
5, 10, 15, 20, 25,
so I can calculate the average of the first 10 terms as
 ,
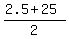and the sum of those  terms as
    .
|
|
|
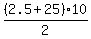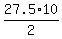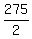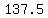