Question 1110010: The xth, yth, and zth terms of a sequence are X,Y,Z respectively. Show that if the sequence is arithmetic then X(y-z) + Y(z-x) + Z(x-y)=0.
Found 2 solutions by AnlytcPhil, Edwin McCravy:
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To avoid getting capital and small letters confused I will
let p=x, q=y, and r=z. Then the problem is:
The pth, qth, and rth terms of a sequence are X,Y,Z respectively. Show that
if the sequence is arithmetic then X(q-r) + Y(r-p) + Z(p-q)=0.
Let the sequence be arithmetic, with first term a
and common difference d, then by the formula for nth term,
we have these three equations:
 Solve the first and second equations for d
Solve the first and second equations for d
 Solve the first and third equations for d
Solve the first and third equations for d
 Since both expressions equal d, they are equal to each other
Since both expressions equal d, they are equal to each other
  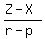 Cross-multiply:
Cross-multiply:




 Edwin
Edwin
|
|
|