Question 1109379: Explicit formula the sequence & 12th term.
2, 6, 12, 20
Am I correct in having the formula be A(n)=n(n+1)?
This would make t he 12th term 156, right?
Thanks
Found 2 solutions by KMST, rothauserc:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! You are correct.
UNREQUESTED NOTES:
You are probably starting to learn about sequences,
and will probably face puzzling problems like that right now.
After the puzzling start, problems become similar to one another,
comfortably boring, and there is less guessing required.
You may be even told to look at differences between consecutive terms
(in this case, 4, 6, 8),
and then second differences (6-8=2, 8-6=2).
If first differences are all the same number  ,
you have what they call an arithmetic sequence,
and terms would have a formula like
 or 
If second differences are all the same number,
there will be an  term in the formula for  .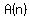
In your case,  .
Answer by rothauserc(4718)  (Show Source):
You can put this solution on YOUR website! 2, 6, 12, 20
:
first level differences are
:
4, 6, 8
:
second level differences are
:
2, 2
:
therefore we know the formula is a quadratic of the form
:
an^2 +bn + c
:
for n=1, we have a +b +c = 2
for n=2, we have 4a +2b +c = 6
for n=3, we have 9a +3b +c = 12
:
we have a system of three equations in three unknowns
:
subtract the first equation from the second and third equations
:
3a +b = 4
8a +2b = 10
:
using the first one, solve for b and substitute in the second one
b = 4-3a
8a +2(4-3a) = 10
:
8a +8 -6a = 10
2a = 2
a = 1
:
substitute for a in 3a +b = 4
:
3(1) + b = 4
b = 1
:
a = 1 and b = 1, therefore
:
c = 0
:
our formula is n^2 +n
:
************************
x(12) = 12^2 + 12 = 156
:
you are correct
************************
:
|
|
|
