SOLUTION: For what values of n will the infinite series (2n-1)+(2n-1)^2+...+(2n-1)^i+... have a finite value

Algebra ->  Sequences-and-series -> SOLUTION: For what values of n will the infinite series (2n-1)+(2n-1)^2+...+(2n-1)^i+... have a finite value      Log On


   

Question 1109139: For what values of n will the infinite series (2n-1)+(2n-1)^2+...+(2n-1)^i+... have a finite value
Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
The sum of an infinite geometric progression converges if and only if the common ratio is less than 1 by the modulus.  In your case it means

|2n -1| < 1,   or,  equivalently,


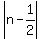abs%28n-1%2F2%29 < 1%2F2.


The solution to the last inequality are all those "n" that are remoted less than 1%2F2  from 1%2F2, i.e.

    0 < n < 1.


Or, in the interval notation,  those "n" that belong to the interval (0,1)   (the ends are not included !).

Solved.