Question 1107236: what is the value of 9^(1/3) x 9^(1/9) x 9^(1/27) x ...?
also is there a general formula in solving these types of question? thanks!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You know that  . .
So,
 , ,
because

That sum is the sum of an infinite geometric sequence.
The "formula" for such a sum with a first term  and a common ratio and a common ratio  is is
 . .
In the case of the sum above, with  and and  , ,
 . .
There is no need to memorize formulas, if you can deduce them.
Consider the sum or  terms terms
 . .
 , and , and
 --> -->  --> -->  . .
If  , we might like to write it as , we might like to write it as
 , ,
and as  approaches approaches  , , 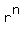 approaches approaches  , ,
and  approaches approaches 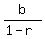 . .
|
|
|