Question 1107227: In an arithmetic series, t5=16 and S10=175, find S25
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For each arithmetic progression, the sum of terms equally remoted from the first and the last terms is the constant value.
In other words, if  , ,  , ,  , . . . , , . . . , 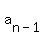 , ,  is an arifmetic progression of n terms, then is an arifmetic progression of n terms, then
 + +  = =  + + 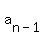 = =  + + 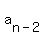 and so on.
For the AP of 10 terms and so on.
For the AP of 10 terms
 + +  = =  + +  = =  + + 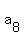 = . . . = = . . . =  + +  .
Hence, the sum .
Hence, the sum  + +  + . . . + + . . . +  is 5 times taken the sum is 5 times taken the sum  + +  : :
 + +  + . . . + + . . . +  = = 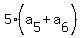 . (1)
This formula is PARALLEL (or similar) to the general formula for the sum of an AP: . (1)
This formula is PARALLEL (or similar) to the general formula for the sum of an AP:  = = 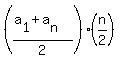 .
From the formula (1) we can find the sum .
From the formula (1) we can find the sum 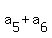 . It is . It is
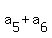 = = 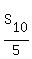 = = 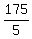 = 35.
We also know that = 35.
We also know that  = 16.
It gives = 16.
It gives  = 35 - 16 = 19.
Thus two neighbor terms of the AP are 16 and 19; they differ by 3 = 19-16, which is the common difference d of the progression.
Having = 35 - 16 = 19.
Thus two neighbor terms of the AP are 16 and 19; they differ by 3 = 19-16, which is the common difference d of the progression.
Having  = 16 and d = 3, we can find = 16 and d = 3, we can find
 = = 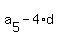 = 16 - 4*3 = 4, = 16 - 4*3 = 4,
 = =  = 4 + 24*3 = 76.
Now, to find = 4 + 24*3 = 76.
Now, to find  , apply the general formula , apply the general formula
 = = 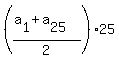 = = 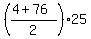 = 1000.
Answer. = 1000.
Answer.  = 1000. = 1000.
Solved.
----------------
There is a bunch of lessons on arithmetic progressions in this site:
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Mathematical induction and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|