SOLUTION: Find the common ratio of a finite geometric series if the first term is 11, and the sum of the first 12 terms is 2922920.

Click here to see ALL problems on Sequences-and-series

Question 1103432: Find the common ratio of a finite geometric series if the first term is 11, and the sum of the first 12 terms is 2922920.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200) (Show Source):
You can put this solution on YOUR website!

If the common ratio is r, then the sum of the first 12 terms is
11+11r+11r^2+...+11r^11 =

I don't know of an algebraic method for solving an equation like that.
Graphing the left and right sides of the equation on a graphing calculator and looking for the intersection shows r=3.

If we assume that the common ratio is a whole number, (almost a certainty, because the sum of the first 12 numbers is a whole number), then rough estimation of the 12th term can give us that answer:
11*2^11 = 11*2048 too small
11*4^11 = 11*2^22 = 11*2048^2 way too big

Answer by ikleyn(52788) (Show Source):
You can put this solution on YOUR website!
.

Let "r" be the unknown common term. Then S = 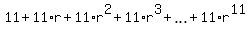= 2922920, which implies 1 + r + r^2 + r^3 + . . . + r^11 = 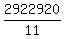= 265720, or 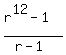= 265720 You can check that r= 3 is the solution to this equation: 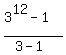= 265720.

Answer. The common ratio of this progression is 3.

--------------

It is not difficult to prove that r= 3 is the UNIQUE solution to the problem. Indeed, if r >=1 then the sum 1 + r + r^2 + . . . + r^11 is monotonic function of r. Next, if 0 < r < 1, then this sum is less than 12. Further, if -1 <= r < 0, then AGAIN this sum is less than 12. Finally, if r < -1, then 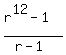has POSITIVE numerator and negative denominator, which means that this rational function is NEGATIVE. The plot below ILLUSTRATES this behavior of the function 1 + r + r^2 + . . . + r^11. Plot y = 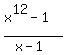(red) and y = 265720 (green)