Question 1102476: The 5th term in a sequence is 25, and each term is 3 less than the previous term. Write an explicit rule and a recursive rule to describe the sequence.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! WITHOUT MEMORIZED FORMULAS:
 or or 
would be the recursive rule spelled out in
"each term is 3 less than the previous term."
Then 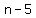 terms after the 5th term, we would have terms after the 5th term, we would have
subtracted from 25 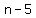 times 3, so times 3, so
 , which simplifies to , which simplifies to
 and to the simplest explicit rule and to the simplest explicit rule
 . .
Your teacher may have in mind a lot of formula memorizing and writing, like
 = common difference. = common difference.
 is the memorizable recursive rule formula for any arithmetic sequence, is the memorizable recursive rule formula for any arithmetic sequence,
so in this case  , ,
or  . .
For all arithmetic sequences,
 is the memorizable explicit rule for any arithmetic sequence. is the memorizable explicit rule for any arithmetic sequence.
For  , with , with  and and  , we can find , we can find  : :




 . .
Plugging 
into the memorized  , we get explicit rule , we get explicit rule
 , ,
not that simple, but maybe the expected answer.
|
|
|