Question 1101405: In the sequence -12, -7, -2, 3, 8, 13,...determine the 90th term and the sum of the first 80 terms.
Found 2 solutions by josgarithmetic, stanbon:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Common difference of 5, increasing sequence.
General term, 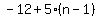 for index, n. for index, n.
You can determine the n=90 term from that.
Sum of first 80 terms:
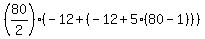 ------simplify and compute this. ------simplify and compute this.
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! In the sequence -12, -7, -2, 3, 8, 13,...determine the 90th term and the sum of the first 80 terms.
----
Arithmetic sequence with d = -7-(-12) = 5 and a(1) = -12
----
a(90) = -12 + (89)5 = 433
-------
Sum of 1st 80::
S(80) = (80/2) * (-12+a(80))
---
But, a(80) = -12 + 79*5 = 383
----
So, S(80) = 40*(-12+383) = 14840
--------------
Cheers,
Stan H.
|
|
|