|
Question 1100391: The sum of an infinite gp is 16 and the sum of the squares of its terms is 768/5. Find common ratio and 4th terms of progression.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The sum of an infinite GP with the first term "a" and the common difference "r", |r| < 1 is  .
Therefore, our first equation for the given GP is .
Therefore, our first equation for the given GP is
 = 16. (1)
The second GP, comprised of the squares of the first GP, has the first term = 16. (1)
The second GP, comprised of the squares of the first GP, has the first term 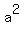 and the common difference and the common difference  .
Therefore, our second equation for the sum of squares is .
Therefore, our second equation for the sum of squares is
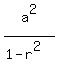 = = 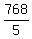 . (2)
Now divide eq(2) by eq(1) (both sides). You will get . (2)
Now divide eq(2) by eq(1) (both sides). You will get
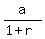 = =  . (3) (Take into account that . (3) (Take into account that 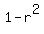 = (1-r)*(1+r))
Next step divide eq(3) by eq(1) (both sides). You will get = (1-r)*(1+r))
Next step divide eq(3) by eq(1) (both sides). You will get
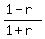 = =  . (4)
Now we are at the finish line. From eq(4), making cross-multiplying, you get
5*(1-r) = 3*(1+r) ====> 5 - 5r = 3 + 3r ====> 5-3 = 3r + 5r ====> 8r = 2 ====> r = . (4)
Now we are at the finish line. From eq(4), making cross-multiplying, you get
5*(1-r) = 3*(1+r) ====> 5 - 5r = 3 + 3r ====> 5-3 = 3r + 5r ====> 8r = 2 ====> r =  .
Thus we just found the common difference of the original progression. It is .
Thus we just found the common difference of the original progression. It is  .
Last step is to find "a": a = 16*(1-r) = .
Last step is to find "a": a = 16*(1-r) = 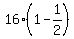 = 8.
Answer. The common ratio is = 8.
Answer. The common ratio is  , the first term is 8, and the 4-th term is , the first term is 8, and the 4-th term is 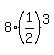 = 1. = 1.
Solved.
---------------
There is a bunch of lessons on geometric progressions in this site
- Geometric progressions
- The proofs of the formulas for geometric progressions
- Problems on geometric progressions
- Word problems on geometric progressions
- One characteristic property of geometric progressions
- Solved problems on geometric progressions
- Fresh, sweet and crispy problem on arithmetic and geometric progressions
- Mathematical induction and geometric progressions
- Mathematical induction for sequences other than arithmetic or geometric
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Geometric progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
================
Thank you, Edwin.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
|
|
|
| |