Question 1100170: In the following two AP's how many terms are identical? 2,5,8,11....to 60 terms, 3,5,7...50 terms.
Found 2 solutions by richwmiller, ikleyn:
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! first AP 2,5,8,11....to 60 terms
2 5 8 11 14 17 20 23 26 29 32 35 38 41 44 47 50 53 56 59 62 65 68 71 74 77 80 83 86 89 92 95 98 101 104 107 110 113 116 119 122 125 128 131 134 137 140 143 146 149 152 155 158 161 164 167 170 173 176 179 ct 60
second AP 3,5,7...50 terms
3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99 101 ct 50
Notice that the second AP are all the odd numbers 3 to 101
So just count the odd numbers in the first AP.
This a method of solution. It is not a solution based on equations and formulas but as Ikleyn often says based on logic. It is certainly an easier method. All you have to do is look for odd numbers
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In the following two AP's how many terms are identical? 2,5,8,11....to 60 terms, 3,5,7...50 terms.
~~~~~~~~~~~~~~~~~
Two progressions have the number 5 common as their second term, in each progression.
Further, the first progression comes with the common difference 3, while
the second progression comes with the common difference 2.
It means that, starting from their common second term of the value 5, they will have these CANDIDATES to be common terms:
- every second term of the first progression.
- every third term of the second progression.
We also should take care that the terms belong to their common range.
The last term of the 1-st AP is 2 + 59*3 = 179.
The last term of the 2-nd AP is 3 + 49*2 = 150.
So, the common range ends at 150.
Thus the amount of common members of the 1-st AP in this common range (starting and including 5)
is the integer part of the number 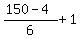 , i.e. 25.
And now calculating the amount of common members of the 2-snd AP in this common range (starting and including 5)
is the integer part of the number , i.e. 25.
And now calculating the amount of common members of the 2-snd AP in this common range (starting and including 5)
is the integer part of the number 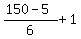 gives the same 25 (ONLY FOR CHECKING).
Answer. These two sequences have 25 numbers in common. gives the same 25 (ONLY FOR CHECKING).
Answer. These two sequences have 25 numbers in common.
I think that the advise of the other tutor TO COUNT MANUALLY the common terms IS NOT THE SOLUTION and IS NOT THE METHOD OF SOLUTION.
|
|
|