Question 1097200: I ONLY NEED TO KNOW PART C
5a. The sides of a square are 16 cm in length. The midpoints of the sides of this square are joined to form a new square and four triangles. The process is repeated twice.
Let Xn denote the length of one of the equal sides of each new triangle.
Let An denote the area of each new triangle.
The following table gives the values of Xn and An, for 1 less than or equal to n less than or equal to 3.
N 1 2 3
Xn 8 __ 4
An 32 16 __
(First blank I got 6, second blank I got 8)
5b. The process described above is repeated. Find A6.
A6 = 8
5c. Consider an initial square of side length k cm. The process describes above is repeated indefinitely. The total area of the shaded regions is k cm^2. Find the value of k.
Found 2 solutions by greenestamps, KMST:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
I ONLY NEED TO KNOW PART C
But your answers for parts A and B are not right....
5a. The sides of a square are 16 cm in length. The midpoints of the sides of this square are joined to form a new square and four triangles. The process is repeated twice.
Let Xn denote the length of one of the equal sides of each new triangle.
Let An denote the area of each new triangle.
The following table gives the values of Xn and An, for 1 less than or equal to n less than or equal to 3.
N 1 2 3
Xn 8 __ 4
An 32 16 __
(First blank I got 6, second blank I got 8) <--- NO; YES
How did you get 6 for X2? Xn is the length of a side of the triangle (short side, not the hypotenuse) at step n.
The areas of the triangles go down by a factor of 2 each time. That is (to me at least) clear from the diagram; it also agrees with your results showing A1=32, A2=16, and A3=8.
The area of each triangle is one-half base times height, which in this problem is one-half the square of the length of the side. So you should always have
If X2 is 6, then A2 would be
but we know it is 16.
5b. The process described above is repeated. Find A6.
A6 = 8
You correctly found A3 to be 8, and the numbers are getting smaller, by a factor of 2 each time. How can A6 be 8?
You know the areas are going down by a factor of 2 each time; if A3 is 8, what will A6 be?
5c. Consider an initial square of side length k cm. The process describes above is repeated indefinitely. The total area of the shaded regions is k cm^2. Find the value of k.
For part C, there is nothing in the statement of the problem that defines which areas are shaded.
I am guessing that the shaded areas are the areas of the triangles. But with the process as described, if it is repeated indefinitely, then the whole original square ends up being shaded.
If that is the right interpretation, then part C is asking for what value of k is the side length of the square in cm equal to the area of the square in square cm. The answer to that is easy: k=1.
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! You need more help than that.
You are half right on question 5a.
As you draw each new square,
the new square area is half of the area of the previous square.
The square can be split into 4 more triangles,
as I did with those green lines,
and the other half of the previous square area is made of the 4 new triangles.
The areas of squares and triangles form a geometric sequence with common ratio 1/2
So, the areas are 32,16,8,4,2,1,1/2,1/4, and so on.
The terms of that sequence are called 
The second blank (area of the third triangle) is indeed  .
Because areas are made by multiplying lengths of sides and a convenient factor,
lengths of sides form a geometric sequence with common ratio
 .
So, the sides are 8,4sqrt(2),4,2sqrt(2),2,sqrt(2),1, and so on.
The terms of that sequence of lengths are called  .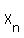
The first blank (side of the second triangle) is not 6, but  .
5b. You may have misinterpreted that question.
The question asks for 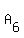 , the 6th term of the sequence of areas that I listed above.
I do not know how you came up with your answer, but the sequence of areas is
32,16,8,4,2,1,1/2,1/4, and so on, and the 6th term there is
 .
5c. You did not include a picture so that we could figure out what area was shaded in the picture that came with your question.
However, I did an internet search using a phrase with your question.
I found the question to show one shaded triangle from the each step,
all adjacent to the triangles in the steps before and after,
forming a clockwise spiral.
The area shaded after an infinite number of steps is the sum of the terms from start to infinity:
32+16+8+4+2+1+....=64.
If you had to "show your work" the teacher may expect you to say that
the areas form a geometric sequence with common ratio  .
and because that ratio is less than 1, the series (the sum) converges to
     .
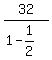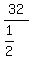However, a fifth grader (or someone smarter than that)
would realize that each sum gets closer to 64,
and that what it needs to get to 64 is exactly the last term added.
Adding we would never get to 64,
because we would need to add infinite terms,
and our lives are finite,
but the sum to infinity is 64,
because we see that  ,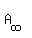
if there was such a real number, would be zero.
If the first square has side length  ,
the area of that square would be  and the area of each of the first set of tr triangles would be
 .
Then the sum of infinite triangles would be  .
If that is equal to ,
 , meaning that if  ,
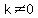and there really was an initial square,
we can divide both sides by to get
 and  .
|
|
|
