SOLUTION: Use mathematical induction to prove 6 is a factor of n^3 + 3n^2 + 2n. Please pls pls pls help me. Thankyou.

1.  According to the Method of Mathematical induction, check the statement at n = 1:

    1^3 + 3*1^2 + 2^1 = 1 + 3 + 2 = 6 

    and the statement is TRUE.



2.  According to the Method of Mathematical induction,  let us assume that the statement is true for n= k, i.e. let assume that 

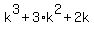      is a multiple of 6.


    Consider the polynomial expression at  n = k+1. You have

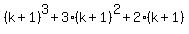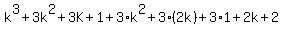     =  = regroup the terms =  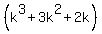+ 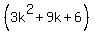.     (1)

    According to the induction assumption, the term 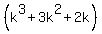   is a multiple of 6.


    The last term 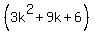  = 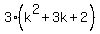 = 3*(k+1)*(k+2)  is the thrice the product of two consecutive integer numbers.

    So, this product is multiple of 2, and when multiplied by 3, is a multiple of 6.


    Thus, the right side of (1) is a multiple of 6,  and the induction step is proved.



3.  According to the principle of the Mathematical induction, the original statement is proved.