Question 1094808: If the sum of three number in geometric series is 14 and their product is 64.find the number
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
2, 4 and 8.
Another progression is 8, 4, 2.
Mental solution. 3 seconds.
-----------
If you want algebra solution, here it is.
Let "a" be the first term and "r" be the common ratio.
Then the terms are a, ar and ar^2.
a + ar + ar^2 = 14, (1)
a * ar * ar^2 = 64 (2)
From (2) you have a^3*r^3 = 64 ====> (ar)^3 = 64 ===> ar = 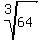 = 4.
Next step substitute ar = 4 everywhere into (1). You will get
a + 4 + 4r = 14, or
a + 4r = 10.
Express a = 10-4r and substitute it into ar = 4.
You will get a quadratic equation
(10-4r)*r = 4.
The rest is just arithmetic.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The first response you got is exactly right: mental arithmetic! Algebra is overkill....
You are given that the product is 64 and the sum is 14. If both product and sum are whole numbers, then it is almost certain that the numbers are whole numbers.
The product, 64 is 2^6; so all three of the numbers have to be powers of 2.
And a little thought shows that the three numbers 2^1=2, 2^2=4, and 2^3=8 satisfy all the conditions of the problem.
|
|
|
