Question 1094327: How many terms from the sequence 5, 1, 0.2, 0.04, .....are needed to form a sum that is within 2.5 x 10^ -8 of the infinite sum?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The infinite sum is

Now look at the sequence consisting of the infinite sum minus the sum of the first n terms of the given sequence. The sums of the first n terms of the given sequence form the sequence
5, 6, 6.2, 6.24, ...
The sequence consisting of the differences between the infinite sum and the terms in this sequence is
1.25, .25, .05, .01, ...
We can see that this sum is a decreasing geometric sequence, with first term 1.25 and common ratio 0.2. We want to know how many terms we need to go out in this sequence to get a number less than 2.5x10^-8. So we need to solve
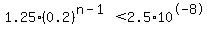
Logarithms and a scientific calculator show that 12 terms is just barely not enough; we need to add 13 terms of the given sequence to get within 2.5*10^-8 of the infinite sum.
|
|
|