Question 1091859: Please help...
I know the arithmetic sequence Sn=n(A1+An)/2, but I cannot solve this problem
Q: nth triangular number = n(n+1)/2,
Prove this formula algebraically using the sum of a finite arithmetic sequence theorem.
Thank you.
Answer by math_helper(2461)   (Show Source):
You can put this solution on YOUR website! The Nth Triangular number is the sum of the sequence of positive integers up to and including N:
Noting that A1 = 1 and An = n:
Tn = 
(you are just picking out one Tn, not the sum of an entire sequence of triangular numbers)
—
That concludes the proof IF you are allowed to use the starting point Sn=n(A1+An)/2.
———
Here is more of a ground-up method that also proves Tn = n(n+1)/2 and then Sn=n(A1+An)/2:
 — also the 1st triangular number
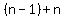 — also the 2nd triangular number
: : :
 + … +  — also the n'th triangular number
—
Looking at 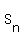 you can take the largest number and pair it with the smallest (1) and form n+1, then (n-2) and 3 to get n+1, etc. You can do this n/2 times*. Thus the sum 1+2+…+n is n(n+1)/2.
—
—
* To see the "n/2 times" because it may not be obvious (also n may be odd) just do this: form the pairs to be summed as (1,n), (2,n-1), (3,n-2), … , (n-2,3), (n-1,2), (n,1) and note that we show each pair TWICE.
The first number in each pair counts how many pairs you have: n
The sum of each pair is: n+1
The sum of all the pairs shown: n*(n+1)
Divide by 2 because we double-counted: Sn = n*(n+1)/2 (done)
—
Proof of Sn = n(A1+An)/2:
Sn = A1+A2+…+An
Pair them up as we did above: (A1,An), (A2,An-1), … ,(An-1,A2), (An,A1)
Thats n pairs.
Sum of each pair is A1+An (A2 + An-1 = A1+An because A2 = A1 + d and An-1 = An - d, similar logic for other pairs)
Adjust for double counting: Sum = n*(A1+An)/2
—
There are other ways to do the proofs, this is just the way I think about it.
|
|
|
