Question 1091579: The difference between two positive numbers is 18 and 4 times their GM is equal to 5 times their HM find the numbers
Found 2 solutions by rothauserc, ikleyn:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) x - y = 18, with x, y > 0
:
GM is geometric mean, GM for x, y is defined as square root (x * y)
:
HM is harmonic mean, HM for x, y is defined as 2 / (1/x + 1/y)
:
2) 4 * square root(x * y) = 5 * (2 / (1/x + 1/y))
:
solve equation 1) for x
:
x = y + 18
:
substitute for x in equation 2
:
4 * square root((y+18) * y) = 5 * (2 / (1/(y+18) + 1/y))
:
4 * square root((y+18) * y) = 10 / (1/(y+18) + 1/y)
:
cross multiply the fractions
:
4 * square root((y+18) * y) * (1/(y+18) + 1/y) = 10
:
divide both sides of = by 4
:
square root((y+18) * y) * (1/(y+18) + 1/y) = 5/2
:
divide both sides of = by (1/(y+18) + 1/y)
:
square root((y+18) * y) = (5y * (y+18)) / (4 * (y+9))
:
square both sides of the =
:
(y+18) * y = (25y^2 * (y+18)^2) / (16 * (y+9)^2
:
cross multiply the fractions
:
16y * (y+18) * (y+9)^2 = 25y^2 * (y+18)^2
:
write the left side of the = in standard form
:
16y^4 +576y^3 +6480y^2 +23328y = 25y^2 * (y+18)^2
:
write the right side of the = in standard form
:
16y^4 +576y^3 +6480y^2 +23328y = 25y^4 +900y^3 +8100y^2
:
consolidate the terms to the left side of =
:
-9y^4 -324y^3 -1620y^2 +23328y = 0
:
this factors into
:
-9y * (y-6) * (y+18) * (y+24) = 0
:
divide both sides of = by -9
:
our solutions for y are 0, 6, -18, -24
:
we reject solutions 0, -18, -24 since y > 0
:
x = 6 + 18 = 24
:
*******************************************
x = 24 and y = 6
*******************************************
:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1) x - y = 18, with x, y > 0. (1)
GM is geometric mean, GM for x, y is defined as 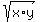 .
HM is harmonic mean, HM for x, y is defined as .
HM is harmonic mean, HM for x, y is defined as 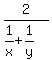 .
2) .
2) 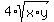 = =  ====> ====>
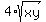 = = 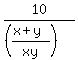 ====> ====>
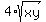 = =  ====> square both sides ====> ====> square both sides ====>
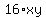 = = 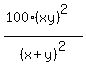 ====> cancel xy in both sides ====>
16 = ====> cancel xy in both sides ====>
16 = 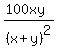 ====> ====> 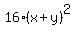 = 100xy ====> = 100xy ====> 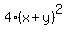 = 25xy (2)
Now from (1) express x = y + 18 and substitute it into (2). You will get = 25xy (2)
Now from (1) express x = y + 18 and substitute it into (2). You will get
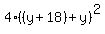 = 25*(y+18)*y, or = 25*(y+18)*y, or
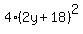 = 25*y*(y+18) ====> = 25*y*(y+18) ====> 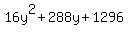 = = 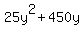 ====> ====> 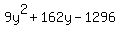 = 0 ====> cancel 9 in both sides ====> = 0 ====> cancel 9 in both sides ====>
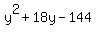 = 0
(y+24)*(y-6) = 0.
Since y must be positive, we have only ONE solution for y: y = 6.
Then x = y + 18 = 24. = 0
(y+24)*(y-6) = 0.
Since y must be positive, we have only ONE solution for y: y = 6.
Then x = y + 18 = 24.
Answer. x = 24, y = 6 is the only solution.
The lesson to learn from this solution:
If you choose the correct way, you reduce the problem to the quadratic equation, and there is no need to solve the equation of degree 4.
|
|
|