.
The sum to infinity of a geometric sequence is 27/2 while the sum of the first three terms is 13. Find the sum of the first 5 terms.
Thank you for your help.
~~~~~~~~~~~~~~~~
We have
S = 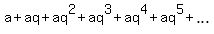 =
= 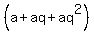 +
+ 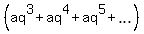 =
= 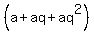 +
+ 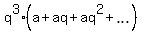 (1)
Notice that the infinite sum in parentheses of the right-most side is S, again. // It is the KEY IDEA #1.
Based on given info, replace in (1) S by
(1)
Notice that the infinite sum in parentheses of the right-most side is S, again. // It is the KEY IDEA #1.
Based on given info, replace in (1) S by  and replace the sum of the first three terms by 13. You will get
and replace the sum of the first three terms by 13. You will get
 =
= 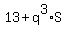 , or, which is the same
, or, which is the same
 =
= 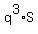 . (2).
In (2), replace S by
. (2).
In (2), replace S by  as it is given. // It is the KEY IDEA #2.
You will get
as it is given. // It is the KEY IDEA #2.
You will get  =
= 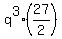 , which implies
, which implies  =
= 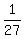 .
Hence, q =
.
Hence, q =  . Thus we just found the common ratio of the progression; it is q =
. Thus we just found the common ratio of the progression; it is q =  .
Now we are at the finish line.
Similar to (1), we have
S =
.
Now we are at the finish line.
Similar to (1), we have
S =  =
=  +
+ 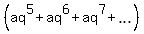 =
=  +
+ 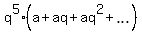 (3)
You can re-write it as
S =
(3)
You can re-write it as
S = 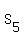 +
+ 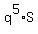 , (4) // It is the KEY IDEA #3.
where
, (4) // It is the KEY IDEA #3.
where 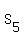 is the sum of the first 5 terms, which is under the question.
Now from (4)
is the sum of the first 5 terms, which is under the question.
Now from (4)
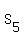 =
= 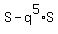 =
= 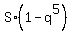 =
= 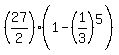 =
= 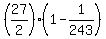 =
=  =
=  =
=  =
= 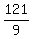 =
= 
 .
.
Answer. The sum of the first 5 terms of the given GP is 
 .
.
******************
***** SOLVED *****
******************