SOLUTION: a*b=62217, c*d=52983, b*c=56637, d*a=58203, b*d=72819, c*a=45269 solve this a+b+c+d=? , A*B*C*D=? , A=?, B=?, C=?,D=?

Algebra ->  Sequences-and-series -> SOLUTION: a*b=62217, c*d=52983, b*c=56637, d*a=58203, b*d=72819, c*a=45269 solve this a+b+c+d=? , A*B*C*D=? , A=?, B=?, C=?,D=?      Log On


   

Question 1088473: a*b=62217, c*d=52983, b*c=56637, d*a=58203, b*d=72819, c*a=45269 solve this a+b+c+d=? , A*B*C*D=? , A=?, B=?, C=?,D=?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

a%2Ab=62217,
c%2Ad=+52983,
b%2Ac=56637,
d%2Aa=58203,
b%2Ad=72819,
c%2Aa=45269
solve this:
a%2Bb%2Bc%2Bd=? ,

since given a%2Ab=62217 and c%2Ad=+52983, we have
A%2AB%2AC%2AD=%28A%2AB%29%2A%28C%2AD%29+=62217%2A52983=3296443311
now, we will find out what are A,B,C,and D equal to:

a%2Ab=62217->b=62217%2Fa.....1)
b%2Ad=72819->b=72819%2Fd....1)
from 1) and 2):
=>62217%2Fa=72819%2Fd=>d%2Fa=72819%2F62217=>d%2Fa=261%2F223=>d=261a%2F223....3)

since d%2Aa=58203 we have d=58203%2Fa....4)

from 3) and 4) we have
261a%2F223+=58203%2Fa............solve for a
a%2Aa%2F223+=58203%2F261
a%5E2=%2858203%2F261%29223+
a%5E2=%28223%29223+
a%5E2=%28223%29%5E2+
highlight%28a=223+%29
find d:
d=261a%2F223....3)
d=%28261%2Across%28223%29%29%2Fcross%28223%29
highlight%28d=261%29


go to a%2Ab=62217, plug in a and find b
223%2Ab=62217
b=62217%2F223
highlight%28b=279%29

go to b%2Ac=56637,plug in b and find c
279%2Ac=56637
c=56637%2F279
highlight%28c=203%29


so, we have:
A=highlight%28a=223+%29

B=highlight%28b=279%29
C=highlight%28c=203%29
D=highlight%28d=261%29
and, finally we can find a%2Bb%2Bc%2Bd
a%2Bb%2Bc%2Bd=223%2B279%2B203%2B261=966
check the product:
A%2AB%2AC%2AD=223%2A279%2A203%2A261=3296443311....confirmed

Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
a*b=62217, c*d=52983, b*c=56637, d*a=58203, b*d=72819, c*a=45269 solve this a+b+c+d=? , A*B*C*D=? , A=?, B=?, C=?,D=?
~~~~~~~~~~~~~~~~~~~~~~~~

I will show you more simple and more straightforward solution. 

0.  First of all,  EITHER  all four numbers a, b, c and d are POSITIVE, OR all four of them are NEGATIVE.

    Indeed, had two numbers a and b, for example, have different signs, their product ab would be negative.

    Since all given values of products are positive, the statement made is true.

    It means that there are two solutions:

         one solution with all four numbers positive, and
         the second solution with all four numbers negative (opposite).

    For simplicity, let us start finding positive solution, and 
        then will take the opposite numbers as the second solution, for completeness.



1.  The most easy question is about the product a*b*c*d. 

    It is equal  a*b*c*d = (a*b)*(c*d) = 62217*52983 = 3296443311.   (1)



2.  Now I want to find the value of "a".

    For it, I will collect all given products that DO NOT CONTAIN the multiplier (the factor) "a".

    b*c = 56637,    (2)

    c*d = 52983,    (3)

    b*d = 72819.    (4)


Now multiply  all three equations (2), (3) and (4) (both sides).  You will get
    
    b%5E2%2Ac%5E2%2Ad%2A2 = 56637*52983*72819,   or

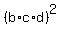    %28b%2Ac%2Ad%29%5E2 = 218515122014049,    which implies (after taking square root of both sides)

    b*c*d = 14782257     (since we are looking now for positive numbers only).


    Then a = 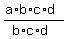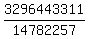%28a%2Ab%2Ac%2Ad%29%2F%28b%2Ac%2Ad%29 = 3296443311%2F14782257 = 223.


4.  Now we will find b, c and d in one line each:

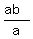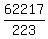    b = %28ab%29%2Fa = 62217%2F223 = 279;

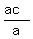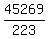    c = %28ac%29%2Fa = 45269%2F223 = 203;   and

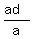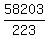    d = %28ad%29%2Fa = 58203%2F223 = 261.


So, there are two answers (two solutions):

    a) a =  223;  b = 279;  c =  203;  d =  261;  a*b*c*d = 3296443311 and a+b+c+d =  966;

    b) a = -223;  b =-279;  c = -203;  d = -261;  a*b*c*d = 3296443311 and a+b+c+d = -966.

Solved.