Question 1088149: Dear Tutor, please help me.
Let A = {(1,2), (2,4), (3,6), (1,4), (2,8), (3,12), (1,3), (2,6), (3,4)}. Let r by the relation defined by (a,b)r(c,d) if and only if ad = bc.
(a) The relation r is reflexive. Give one example of two elements of r (not A ) that demonstrate the reflexive property. Show clearly that the elements you choose satisfy the reflexive property.
(b) The relation r is symmetric. Give one example of two elements of r (not A) that demonstrate the symmetric property. Show clearly that the elements you choose satisfy the symmetric property.
(c) The relation r is transitive. Give one example of three elements of r (not A) that demonstrate the transitive property. Show clearly that the elements you choose satisfy the transitive property.
(d) As r is reflexive, symmetric and transitive it follows that r is an equivalence relation. What are the equivalence classes of r ?
Thank you.
Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website! .
Let me to educate you a bit (a little).
The equality ad = bc means that the determinant of the matrix 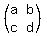 is equal to zero. (*)
This equality also means that the vectors (a,b) and (c,d) are proportional. (**)
These (*) and (**) are EQUIVALENT properties.
Having this HINT will help you easily answer your questions.
a) Regarding "reflexivity" property
The property (the term) "reflexive" means that element E satisfies the relation ErE.
ANY element of your list satisfies this property.
By the way, to check whether this property is valid, you DO NOT NEED to treat two different elements of your set.
The reflexive property must be checked for EACH element individually, not for the pair of elements.
In this sense the formulation a) in your post IS INCORRECT.
b) Regarding "symmetric" property
The example of two elements that demonstrate the symmetric property is
(1,2) and (2,4).
You may check it immediately, making the necessary calculations manually.
c) Regarding "transitivity" property.
The property (**) makes transitivity OBVIOUS in this case:
If vector A is proportional to vector B, And B is proportional to C, then CLEARLY A is proportional to C
and the transitivity is on the place.
d) Regarding classes of equivalency.
The element (1,2) has equivalent (2,4), (3,6). (1)
The element (1,4) has equivalent (2,8), (3,12). (2)
The element (1,3) has equivalent (2,6). (3)
The element (3,4) is equivalent to itself and to nothing else. (4)
So, the lists (1), (2), (3) and (4) represent four classes of equivalency.
Solved.
|
|
|
