Question 1081636: a1=2/5;an=5an−1
an=?
I would dearly love if you can answer in less than a 5 hours please and thanks veryy much!!
Found 3 solutions by stanbon, MathTherapy, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a1=2/5;an=5an-1
an=?
I would dearly love if you can answer in less than a 5 hours please and thanks veryy much!!
~~~~~~~~~~~~~~~~~~~~
These formulas,  = =  and and  = = 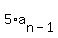 , determine a geometric progression with the first term , determine a geometric progression with the first term  = =  and the common ratio of 5.
The first terms are and the common ratio of 5.
The first terms are
 , 2, 10, 50, 250, . . .
The formula for the n-th term is , 2, 10, 50, 250, . . .
The formula for the n-th term is
 = = 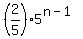 , n = 1, 2, 3, . . .
This formula is what you want. , n = 1, 2, 3, . . .
This formula is what you want.
Solved.
There is a bunch of lessons on geometric progressions in this site
- Geometric progressions
- The proofs of the formulas for geometric progressions
- Problems on geometric progressions
- Word problems on geometric progressions
- One characteristic property of geometric progressions
- Solved problems on geometric progressions
- Fresh, sweet and crispy problem on arithmetic and geometric progressions
- Mathematical induction and geometric progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Geometric progressions".
|
|
|