Question 1075196: Hello,
could I please have some help with this question,
Prove by mathematical induction that;
(1 × 2) + (3 × 4) + · · · + (2n − 1) × 2n = n(n + 1)(4n − 1)/3
for all n ∈ N.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The left hand side of the equation is the sum of
 products of the form products of the form 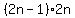 , ,
starting from  . .
You need to prove that
1) it is true for  , the fisrt natural number in N. , the fisrt natural number in N.
2) If it is true for  , it must be true for , it must be true for  . .
1) For  the equation becomes the equation becomes
The equation becomes
 <---> <--->  , ,
which is obviously true.
2) For  the equation becomes the equation becomes
 . .
The sum on the left hand sides has  terms, terms,
If the formula you want to prove is true for  , ,
those  terms add to terms add to 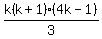 . .
For  the equation becomes the equation becomes

and that is what you have to prove, staring from
 . .
The sum on the left hand sides have the same first  terms terms
up to  , the term number , the term number  , ,
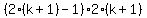
Starting from
 , ,
lets add 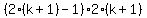 to both sides of the equal sign. to both sides of the equal sign.
 . .
Now the left hand side looks like the sum of 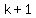 terms you want. terms you want.
If you get the right hand side to look like
 , ,
you have proven part 2), so it's just a little algebra from now on.
 . .
 . .
The sum on the left hand sides has  terms, terms,
If the formula you want to prove is true for  , ,
those  terms add to terms add to 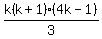 . .





At this point, you realize that  , ,
so it's already really proven that
if the formula you had to prove works for 
it must work for  . .
You can continue, writing
 , ,
 and and
 . .
|
|
|