Question 1074390: If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23. Find the sum of all the multiples of 3 or 5 below 4133.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9.
The sum of these multiples is 23. Find the sum of all the multiples of 3 or 5 below 4133.
~~~~~~~~~~~~~~~~~~~~~
1. Take the sum 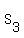 of all integer numbers multiple of 3 from 1 to 4133.
It is the sum of an AP with the first term 3, the common difference 3 and the last term of 4131.
The number of terms is n = of all integer numbers multiple of 3 from 1 to 4133.
It is the sum of an AP with the first term 3, the common difference 3 and the last term of 4131.
The number of terms is n = 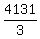 = 1377.
2. Take the sum = 1377.
2. Take the sum 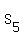 of all integer numbers multiple of 5 from 1 to 4133.
It is the sum of an AP with the first term 5, the common difference 5 and the last term of 4130.
The number of terms is n = of all integer numbers multiple of 5 from 1 to 4133.
It is the sum of an AP with the first term 5, the common difference 5 and the last term of 4130.
The number of terms is n = 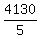 = 826.
3. Calculate = 826.
3. Calculate 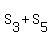 .
Still, it is NOT your answer.
4. To get the answer, distract from .
Still, it is NOT your answer.
4. To get the answer, distract from 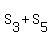 the sum the sum 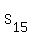 of all integer numbers multiple of 15 from 1 to 4133.
( Since you counted these numbers TWICE in the sum of all integer numbers multiple of 15 from 1 to 4133.
( Since you counted these numbers TWICE in the sum 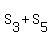 (!) )
The sum (!) )
The sum 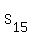 is the sum of an AP with the first term 15, the common difference of 15 and the last term 4125.
The number of terms is n = is the sum of an AP with the first term 15, the common difference of 15 and the last term 4125.
The number of terms is n = 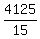 = 275.
5. Again, your answer will be = 275.
5. Again, your answer will be 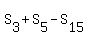 .
Do all these calculations on your own.
You have clear instructions. The rest is simple arithmetic. .
Do all these calculations on your own.
You have clear instructions. The rest is simple arithmetic.
On calculating the sum of an arithmetic progression see the lesons
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If we find the sum of all the multiples of 3 below 4133,
and add that to the sum of all the multiples of 5 below 4133,
we will have added the multiples of 15 below 4133 twice. So
then if we subtract the sum of all the multiples of 15 from
that we'll have the desired sum.
We find the sum of the multiples of 3 below 4133:
The least multiple of 3 below 4133 is 3.
4133/3 = 1377.67 so the largest multiple of 3 less that 4133
is 1377*3 or 4131.
We want the sum of the arithmetic sequence:
3,6,9,...,4131
We use the sum formula
 We need a1=3 and an=4131
It's obvious to me that the number of terms is n = 1377, but if
it's not obvious to you, just divide them all by 3 and
get the sequence
1,2,3,...,1377
and now you can see that indeed n = 1377.
We substitute in the sum formula
We need a1=3 and an=4131
It's obvious to me that the number of terms is n = 1377, but if
it's not obvious to you, just divide them all by 3 and
get the sequence
1,2,3,...,1377
and now you can see that indeed n = 1377.
We substitute in the sum formula
 --------------------
We find the sum of the multiples of 5 below 4133:
The least multiple of 5 below 4133 is 5.
4133/5 = 826.6 so the largest multiple of 3 less that 4133
is 826*5 or 4130.
We want the sum of the arithmetic sequence:
5,10,15,...,4130
We use the sum formula again:
--------------------
We find the sum of the multiples of 5 below 4133:
The least multiple of 5 below 4133 is 5.
4133/5 = 826.6 so the largest multiple of 3 less that 4133
is 826*5 or 4130.
We want the sum of the arithmetic sequence:
5,10,15,...,4130
We use the sum formula again:
 We need a1=5 and an=4130
As before, it's obvious to me that the number of terms is
n = 826, but again, if it's not obvious to you, just divide
them all by 5 and get the sequence
1,2,3,...,826
and now you can see that indeed n=826.
We substitute in the sum formula
We need a1=5 and an=4130
As before, it's obvious to me that the number of terms is
n = 826, but again, if it's not obvious to you, just divide
them all by 5 and get the sequence
1,2,3,...,826
and now you can see that indeed n=826.
We substitute in the sum formula
 ---------------------------
We find the sum of the multiples of 15 below 4133:
The least multiple of 15 below 4133 is 15.
4133/15 = 275.33 so the largest multiple of 15 less that 4133
is 275*15 or 4125.
We want the sum of the arithmetic sequence:
15,30,45,...,4125
We use the sum formula
---------------------------
We find the sum of the multiples of 15 below 4133:
The least multiple of 15 below 4133 is 15.
4133/15 = 275.33 so the largest multiple of 15 less that 4133
is 275*15 or 4125.
We want the sum of the arithmetic sequence:
15,30,45,...,4125
We use the sum formula
 We need a1=15 and an=4125
Once more, it's obvious to me that the number of terms is
n = 275, but if it's not obvious to you, just divide them all
by 15 and get the sequence
1,2,3,...,275
and now you can see that indeed n=275.
We substitute in the sum formula
We need a1=15 and an=4125
Once more, it's obvious to me that the number of terms is
n = 275, but if it's not obvious to you, just divide them all
by 15 and get the sequence
1,2,3,...,275
and now you can see that indeed n=275.
We substitute in the sum formula
 -----------------------------------------------
So we add the sum of the multiples of 3 and the sum of the
multiples of 5, and get 2846259+1707755 = 4554014
That adds the multiples of 15 twice, since multiples of 15
are multiples of both 3 and 5.
So we subtract the sum of the multiples of 15 and get
4554014-569250 = 3984764 <-- answer
Edwin
-----------------------------------------------
So we add the sum of the multiples of 3 and the sum of the
multiples of 5, and get 2846259+1707755 = 4554014
That adds the multiples of 15 twice, since multiples of 15
are multiples of both 3 and 5.
So we subtract the sum of the multiples of 15 and get
4554014-569250 = 3984764 <-- answer
Edwin
|
|
|