Question 1073587: The first and second terms of a geometric progression are cos θ and sin θ respectively.
(a) Find the common ration r and the third term of this geometric progression in terms of θ.
(b) Given that the first and third terms of this geometric progression and tan θ are three consecutive terms of an arithmetic progression, find the general solution for θ. Give your answer in radians correct to two decimal places.
(c) Suppose that 0 < r < 1. Find the sum to infinity of the geometric progression in this case.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = the first term in a geometric progression = the first term in a geometric progression
 = the second term term in the same geometric progression. = the second term term in the same geometric progression.
(a) The common ratio,  in a geometric progression is the ratio of one term to the next, in a geometric progression is the ratio of one term to the next,
one term divided by the term before. In this case

The third term is
 . .
(b) So the first three terms of the arithmetic progression in this problem are
 , ,
 and and
 . .
The common difference is
 , ,
but it is also
 . .
So, our equation is
 . .
Solving:







I am tired of writing  so many times. so many times.
I will abbreviate it as  for a while. for a while.
(It's what the teacher would call a change of variable).
Now the equation is
 <---> <--->  , ,
and I can solve it using the quadratic formula


 . .
That yields two solutions for  . .
The approximate values are
 and and
 . .
since both are between  and and  , ,
they both could be  for some for some  . .
Using the inverse function of sine, in radians, I find that
 and and
 . .
The inverse sine function gives you the solutions in quadrants 1 and 4,
but we know that  , ,
so that would give us two more solutions:
 in quadrant 2, and in quadrant 2, and
 in quadrant 3, in quadrant 3,
for a total of 4 solutions, one per quadrant.
There is an infinity number of other solutions,
because adding an integer number  of whole turns to an angle, of whole turns to an angle,
you get a co-terminal angle that has the same values for all its trigonometric functions.
So, the general solutions are



 . .
NOTE:
There are other ways to write the solution.
I could use  for the quadrant 4 solution, if I di not like to see negative numbers. for the quadrant 4 solution, if I di not like to see negative numbers.
I could use 3.14 for  , but then as {{k}}} increases the general solution would not be "correct to two decimal places." , but then as {{k}}} increases the general solution would not be "correct to two decimal places."
I could have two formulas if I consolidate quadrants,
because  and and 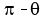 can be written can be written
(in one cumbersome expression) as
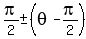 . .
(c) The sum to infinity of a geometric progression
with first term  and and 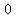 is is
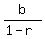 . .
Is this part supposed to be connected to part (b)?
I suppose so. This is almost as evil a problem as the high school comprehensive finals I used to have in Uruguay.
We could conceive that 
That means quadrants 1 or 3 for a positive tangent, and
 --> -->  . .
Considering that and the solutions to part (b) above,
 does not work, does not work,
but  would work would work
for a quadrant 3 angle, with  . .
Hopefully an approximate solution would be OK.
In that case, using  , ,
and  , we get , we get
  . .
|
|
|