SOLUTION: The sum of the fifth and seventh terms of an arithmetic series is 38,while the sum of the first fifteen terms is 375. Determine the first term and the common difference

Algebra ->  Sequences-and-series -> SOLUTION: The sum of the fifth and seventh terms of an arithmetic series is 38,while the sum of the first fifteen terms is 375. Determine the first term and the common difference       Log On


   

Question 1066380: The sum of the fifth and seventh terms of an arithmetic series is 38,while the sum of the first fifteen terms is 375.
Determine the first term and the common difference

Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Assuming you mean, "sequence" instead of "series".

General term:
a%2B%28n-1%29d
Index is n;
common difference each next term is d.

%28a%2B4d%29%2B%28a%2B6d%29=38
2a%2B10d=38
a%2B5d=19

Sum of first fifteen terms
15%28a%2Ba%2B%2815-1%29d%29%2F2=375

%2815%2F2%29%282a%2B14d%29=375

15%28a%2B7d%29=375

a%2B7d=25

Simplified system is system%28a%2B5d=19%2Ca%2B7d=25%29.
Solve this system.

Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
The sum of the fifth and seventh terms of an arithmetic series is 38,while the sum of the first fifteen terms is 375.
Determine the first term and the common difference
~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

1.  %28a%5B5%5D%2Ba%5B7%5D%29%2F2 = a%5B6%5D.   (1)


    Indeed, 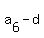a%5B5%5D = a%5B6%5D+-d+,
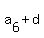            a%5B7%5D = a%5B6%5D+%2B+d.

    Adding, you get (1).

    It is a general (and characteristic) property of any arithmetic progression:


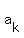            for any three consecutive terms  a%5Bk-l%5D,  a%5Bk%5D and  a%5Bk%2Bl%5D  the middle term is equal to the half-sum of its neighbors.

            See the lesson One characteristic property of arithmetic progressions in this site.


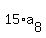2.  a%5B1%5D+%2B+a%5B2%5D+%2B+a%5B3%5D+%2B+ellipsis+%2B+a%5B15%5D = 15%2Aa%5B8%5D.


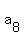    It is easy to prove expressing the terms as neighbors of the central term a%5B8%5D:

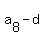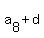    a%5B7%5D = a%5B8%5D-d,    a%5B9%5D = a%5B8%5D%2Bd,
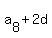    a%5B6%5D = a%5B8%5D-2d,   a%5B9%5D = a%5B8%5D%2B2d,
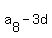    a%5B5%5D = a%5B8%5D-3d,   a%5B9%5D = a%5B8%5D%2B3d,
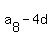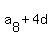    a%5B4%5D = a%5B8%5D-4d,   a%5B9%5D = a%5B8%5D%2B4d,
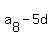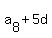    a%5B3%5D = a%5B8%5D-5d,   a%5B9%5D = a%5B8%5D%2B5d,
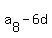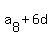    a%5B2%5D = a%5B8%5D-6d,   a%5B9%5D = a%5B8%5D%2B6d,
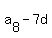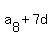    a%5B1%5D = a%5B8%5D-7d,   a%5B9%5D = a%5B8%5D%2B7d,

and then adding the terms.

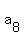    Hense, a%5B8%5D = 375%2F15 = 25.     (2)


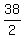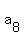3.  Thus from (1) we have a%5B6%5D = 38%2F2 = 19.   From (2),  a%5B8%5D = 25.

    From this, we immediately have 2d = 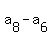a%5B8%5D-a%5B6%5D = 25-19 = 6.

    Hence, the common difference d = 6/2 = 3.


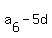4.  Then a%5B1%5D = a%5B6%5D-5d = 19 - 5*3 = 19 - 15 = 4.

Answer. a%5B1%5D = 4; d = 3.

The lesson to learn from this solution: Sometimes, it is useful to think,
                    whether is it possible to build the solution around the properties of the central term of an arithmetic progression.


-------------------------
There is a bunch of lessons on arithmetic progressions in this site:
    - Arithmetic progressions
    - The proofs of the formulas for arithmetic progressions
    - Problems on arithmetic progressions
    - Word problems on arithmetic progressions
    - Mathematical induction and arithmetic progressions
    - One characteristic property of arithmetic progressions
    - Solved problems on arithmetic progressions


Also, you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".